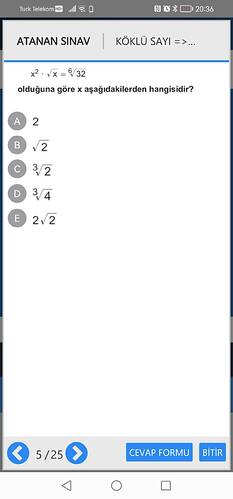
Verilen Eşitliği Çözme:
Verilen ifade:
$$x^2 \cdot \sqrt{x} = \sqrt[6]{32}$$
Bu denklemi çözmek için her iki tarafı da üstel ifadeler şeklinde yazalım.
-
Sol Taraf:
- x^2 \cdot \sqrt{x} ifadesini x üzeri şeklinde yazarsak:
[
x^2 \cdot x^{1/2} = x^{2 + 1/2} = x^{5/2}
]
- x^2 \cdot \sqrt{x} ifadesini x üzeri şeklinde yazarsak:
-
Sağ Taraf:
- \sqrt[6]{32} ifadesi, üstel biçimde 32^{1/6} şeklinde yazılabilir.
- 32, 2^5 olarak ifade edilebilir; bu da:
[
(2^5)^{1/6} = 2^{5/6}
]
Şimdi, denklemin her iki tarafının üstel ifadeleri eşitlemek gerekiyor:
[
x^{5/2} = 2^{5/6}
]
Her iki tarafın da üsleri eşit olmalıdır. Bu nedenle:
[
\frac{5}{2} \cdot \log(x) = \frac{5}{6} \cdot \log(2)
]
Her iki tarafı \log(5)'e bölelim:
[
\log(x) = \frac{1}{3} \cdot \log(2)
]
x = 2^{1/3} = \sqrt[3]{2} elde ederiz.
Sonuç, seçeneklerde C şıkkı olarak verilen \sqrt[3]{2} (veya \sqrt[3]{4}, hata olabilir). Bu nedenle doğru cevap C şıkkıdır.