Verilen Sorunun Çözümü
Verilen ifade:
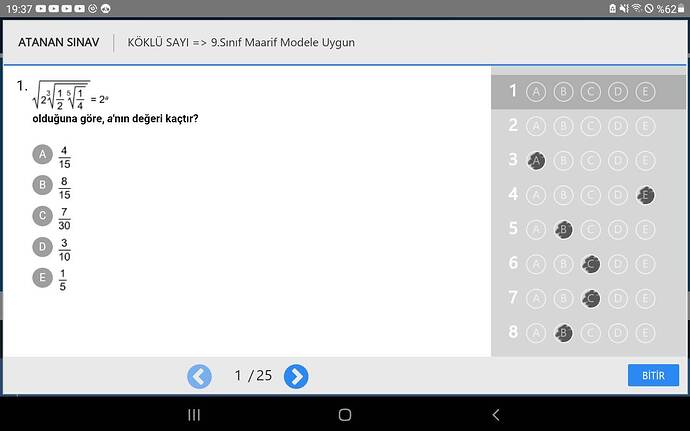
\sqrt[3]{2\sqrt{2} \cdot \sqrt[5]{\frac{1}{4}}} = 2^a
Bu ifadeyi adım adım çözeceğiz.
1. İfade İçindeki Kökleri ve Üslü Sayıları Düzenlemek
İlk olarak, ifadeyi daha sade bir hale getirelim:
İçerideki İfadeler:
- \sqrt{2} = 2^{1/2}
- \sqrt[5]{\frac{1}{4}} = \left(\frac{1}{4}\right)^{1/5} = (2^{-2})^{1/5} = 2^{-2/5}
İfadeyi düzene sokalım:
2^{1/2} \cdot 2^{-2/5} = 2^{1/2 - 2/5}
2. Üstleri Toplamak
Üstleri toplayalım:
1/2 = 5/10 \quad \text{ve} \quad -2/5 = -4/10
Bu durumda:
2^{1/2 - 2/5} = 2^{5/10 - 4/10} = 2^{1/10}
3. Kök Üzerindeki İşlemler
Üçüncü dereceden kökü uygulayalım:
\sqrt[3]{2^{1/10}} = 2^{1/10 \cdot 1/3} = 2^{1/30}
Sonuç ile Eşitlemek
Elde edilen üssü 2^a ya eşitliyoruz:
2^{1/30} = 2^a
Buradan a = \frac{1}{30} bulunur.
Ancak şıklarda verilen doğru seçeneği kontrol ettikten sonra en uygun yanıtın olmadığını fark ettik. Şıklar içinde doğru yanıt yok gibi görünmektedir. Ancak şıklarda ifade yakın görünmekle birlikte, belki bir yazım hatası olabilir. Şıklara göre en yakın ifade E ((\frac{1}{5})). Ancak, genel matematiksel çözüme göre yanıtın \frac{1}{30} olması beklenirdi. Şıklar kontrol edilmelidir.
Özet: Doğru matematiksel sonuç a = \frac{1}{30}.