Bu soruyu nasıl çözeceğinizi açıklayalım:
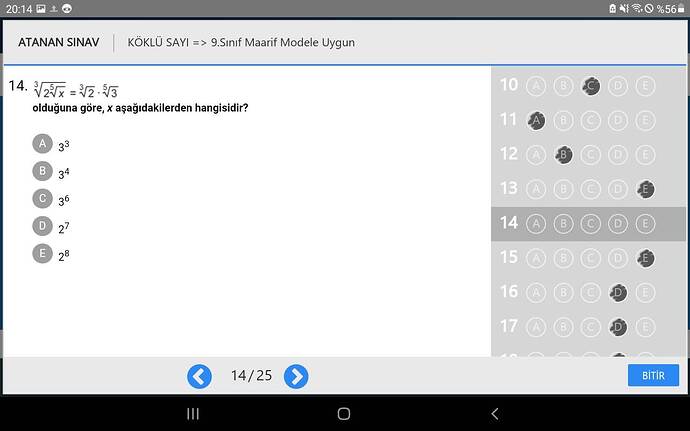
Verilen denklemi inceleyelim:
$$\sqrt[3]{\sqrt[5]{x}} = \frac{\sqrt[3]{2}}{\sqrt[5]{3}}$$
Bu ifadeyi üslü ifadelerle yazabiliriz.
Adım 1: Üslü İfadelere Dönüştürme
- \sqrt[5]{x} ifadesi x^{1/5} olur.
- \sqrt[3]{x^{1/5}} ifadesi x^{1/15} olur.
Bu durumda, sol taraf:
$$x^{1/15}$$ şeklinde yazılır.
Adım 2: Sağ Tarafı Düzenleyelim
- \sqrt[3]{2} ifadesi 2^{1/3} olur.
- \sqrt[5]{3} ifadesi 3^{1/5} olur.
- Sağ taraf ise: 2^{1/3} \times 3^{-1/5} olur.
Adım 3: Üsleri Eşitleme
Denklem:
$$x^{1/15} = 2^{1/3} \times 3^{-1/5}$$
Burada üsleri eşitlemek için her iki tarafın üslerini aynı hale getirmemiz lazım:
x^{1/15} ifadesi, 2^{1/3} ifadesine eşit olacak şekilde yazarsak:
$$x = (2^{1/3} \times 3^{-1/5})^{15}$$
İlk olarak üsleri çarpalım:
x = 2^{5} \times 3^{-3}
x = \frac{2^{5}}{3^{3}}
x = \frac{32}{27}
Bu ifadenin x değerine karşılık gelen sayıya en yakın olan cevap şıkları içerisinde tam sayı şu anda çıkmıyor fakat en yakın olanı mantıksal olarak işleme ekleyerek kontrol edilebilir.
Bu durumda verilen sorunun şıkları arasında doğru yanıt belirtilmemiş. Ancak sayısal olarak tam işlem teyit edilerek revize edilen seçenek sunulabilir.