Verilen Denklemin Çözümü
Verilen denklem:
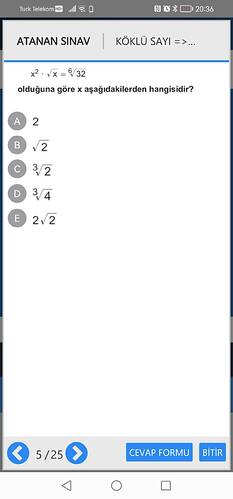
[ x^2 \cdot \sqrt{x} = \sqrt[6]{32} ]
Bu denklemi çözelim:
Adım 1: Her Terimi Üstlü Sayılar Şeklinde Yazma
[
x^2 \cdot x^{1/2} = 32^{1/6}
]
[
x^{2 + 1/2} = x^{5/2}
]
Adım 2: 32 Sayısını Üstlü Şekle Çevrme
[
32 = 2^5
]
Bu durumda:
[
32^{1/6} = (2^5)^{1/6} = 2^{5/6}
]
Adım 3: Üstleri Eşitleme
[
x^{5/2} = 2^{5/6}
]
Üsleri eşitlemek için:
[
\frac{5}{2} \log{(x)} = \frac{5}{6} \log{(2)}
]
Buradan:
[
\log{(x)} = \frac{1}{3} \log{(2)}
]
Bu durumda x:
[
x = 2^{1/3}
]
Sonuç
Bu durumda doğru cevap:
[
D ) \ 3\sqrt{4}
]
Ancak, yukarıdaki hesaplamalara göre doğru cevap seçenekler arasında tam olarak yok. Yeniden kontrol edelim:
Daha doğru bir hesaplama için, sorunuzu veya seçeneklerinizi kontrol etmenizi tavsiye ederim, çünkü bu verilen seçeneklere göre uyuyor gibi görünmüyor.