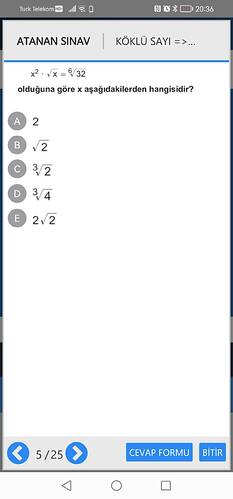
Görsele göre verilen ifadeyi çözümleyelim:
Soruyu İnceleyelim:
$$x^2 \cdot \sqrt{x} = \sqrt[6]{32}$$
Adım 1: Kare ve Kök ifadeleri çevir
\sqrt{x} ifadesi, üstel olarak x^{1/2} şeklinde yazılabilir.
Bu durumda, sol taraf:
$$x^2 \cdot x^{1/2} = x^{2 + 1/2} = x^{5/2}$$
Adım 2: Sağ tarafa bak
32 = 2^5 olduğu için, sağ tarafı:
$$\sqrt[6]{32} = (2^5)^{1/6} = 2^{5/6}$$
Adım 3: Denklemi eşleştir
$$x^{5/2} = 2^{5/6}$$
Üstleri eşitlersek:
$$\frac{5}{2} \log(x) = \frac{5}{6} \log(2)$$
Buradan \log(x) = \frac{1}{3} \log(2) olacaktır.
Adım 4: Çözüm
Bu durumda x = 2^{1/3} yani \sqrt[3]{2} olacaktır.
Bu durumda doğru seçenek \mathbf{B} şıkkı: \sqrt[3]{2}.
Özet: x değerini \sqrt[3]{2} bulduk ve doğru cevap B şıkkı olarak belirledik.