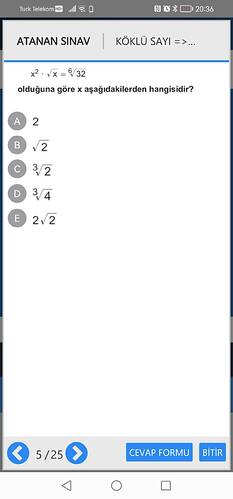
Bu sorunun ne anlama geldiğini açıklayabilir misin?
Tabii ki! Soruda verilen ifade ve çözümleme şu şekilde:
Verilen:
[ x^2 \cdot \sqrt{x} = \sqrt[6]{32} ]
Bu ifadeyi çözmek için öncelikle her iki tarafı üslü sayı olarak yazabiliriz.
Sol taraf:
[ x^2 \cdot x^{1/2} = x^{2 + 1/2} = x^{5/2} ]
Sağ taraf:
[ \sqrt[6]{32} = 32^{1/6} ]
Şimdi eşitliği kurabiliriz:
[ x^{5/2} = 32^{1/6} ]
Üslü denklemin her iki tarafında aynı üsleri kullanalım:
[ (x^{5/2})^{6} = (32^{1/6})^{6} ]
[ x^{15} = 32 ]
32’yi 2 tabanında yazabiliriz:
[ 32 = 2^5 ]
Dolayısıyla:
[ x^{15} = 2^5 ]
Her iki tarafın üstü 15. kökle alınırsa:
[ x = 2^{5/15} = 2^{1/3} ]
Bu durumda x, 2’nin küp köküdür.
Bununla hangi seçeneğin doğru olduğunu kontrol edelim. Doğru cevap:
[ \boxed{\text{C. } \sqrt[3]{2}} ]
Özet: Verilen üslü ve köklü ifadeleri denkleştirerek çözümledik ve x = \sqrt[3]{2} sonucuna ulaştık.