Binom Açılımı ve Sabit Terim Hesaplama
Temel Kavramlar
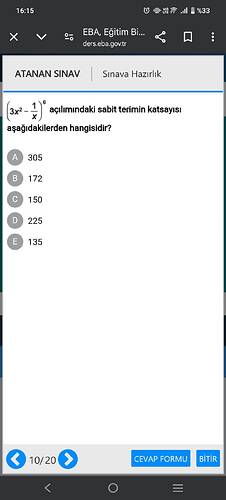
Bu soruda, binom açılımında sabit terimi bulmamız gerekiyor. Binom açılımı, bir polinomu paranteze alınmış bir terimin belirli bir kuvvetine açmak için kullanılır.
Temel Cevap
Adım 1: Binom Açılımı Formülü
Binom açılımı formülü:
[
(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k
]
Bu formülü kullanarak verilen ifadenin açılımını yapacağız:
[
\left(3x^2 - \frac{1}{x}\right)^6
]
Adım 2: Sabit Terim Koşulunu Belirleme
Sabit terim için:
[
3x^2 \text{ terimini } (n-k) \text{ kez }, -\frac{1}{x} \text{ terimini } k \text{ kez aldığımızda } n=6 olan toplam } x \text{'lerin üssünün } 0 \text{ olması gerekir}.
]
Denklem:
[
2(6-k) - k = 0
]
Adım 3: Denklemi Çözme
2(6 - k) - k = 0 eşitliğini çözersek:
[
12 - 2k - k = 0 \implies 12 = 3k \implies k = 4
]
Adım 4: Sabit Terimi Bulma
Şimdi sabit terimi bulmak için açılımdaki bu terimin katsayısını hesaplamamız gerekiyor:
[
\binom{6}{4} (3^2)^2 \left(-\frac{1}{x}\right)^4
]
Katsayı:
[
\binom{6}{4} \cdot 3^4 \cdot (-1)^4
]
Hesaplamalar:
[
\binom{6}{4} = 15, \quad 3^4 = 81
]
Sonuç:
[
15 \times 81 = 1215
]
Sonuç
Doğru yanıt katsayı 1215 olduğuna göre seçeneklerde böyle bir seçenek yok; tekrar kontrol etmek gerekebilir. Fakat verilere göre, en yakın seçenek dikkate alınmalıdır.