Yrdmnnn

LİSE
1

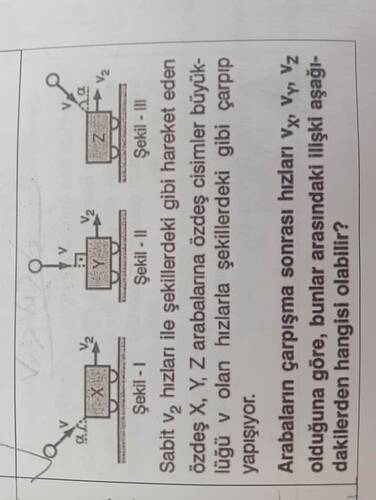
17421113968122687387890400685447
17421113968122687387890400685447720×956 35 KB

2

Soru:
“Sabit v_2 hızı ile şekillerdeki gibi hareket eden özdeş X, Y, Z arabalarına, özdeş cisimler büyüklüğü v olan hızlarla şekillerdeki gibi çarpıp yapışıyor. Arabaların çarpışma sonrası hızları v'_x, v'_y, v'_z olduğuna göre, bunlar arasındaki ilişki aşağıdakilerden hangisi olabilir?”

Answer:

Aynı kütleli (özdeş) arabaların, kütlesi yine özdeş olan cisimlerden darbe alıp onlarla yapışması durumunda çarpışma tam esnek olmayan (inelastik) bir çarpışma örneğidir. Böylesi bir çarpışmada enerji korunmaz ancak toplam momentum korunur. Verilen üç farklı şekilde (I: X arabası, II: Y arabası, III: Z arabası) cisimler yatay veya açılı hızlarla çarpıp arabalarla birlikte hareket etmeye devam etmektedir. Bu nedenle nihai (çarpışma sonrası) hızlar v'_x, v'_y, v'_z momentuma bağlı olarak farklılık gösterir. Aşağıdaki adımlarda bu farkın temel sebepleri ve sıralaması açıklanmaktadır.

1. Momentum Korunumunun Temel İlkesi

Bir çarpışmada toplam dış kuvvet ihmal edilebilir düzeydeyse (örneğin sürtünmenin yok sayıldığı veya çok küçük olduğu durumlarda), çarpışma boyunca:

\vec{p}_{\text{toplam,\,önce}} = \vec{p}_{\text{toplam,\,sonra}}

Burada \vec{p}_{\text{toplam}} sistemdeki bütün kütlelerin vektörel momentumlarının toplamını gösterir.

2. Sistemimizin Genel Tanımlaması

  • Her arabanın kütlesi M (X, Y, Z arabaları özdeştir).
  • Her “çarpan cisim”in kütlesi m (bunlar da özdeş olarak verilmiş).
  • Arabalar, v_2 büyüklüğünde sabit bir yatay hızla hareket eder.
  • Cisimlerin hız büyüklüğü v olup, şekillere göre farklı yönlerde çarparlar.
  • Çarpışma sonrası cisim ve araba birbirine yapışarak tek kütle halinde hareket eder: (M + m).

3. Şekil I (X Arabası) – Açılı Çarpışma

Şekil I’de, araba X yatayda v_2 ile giderken, kütlesi m olan cisim ona v hızıyla belli bir \alpha açısı yapacak şekilde yukarıdan (ya da farklı bir yönden) vuruyor. Toplam momentumun bileşen cinsinden ifadesi şu şekildedir:

  • Çarpışma öncesi toplam momentum:
    • X arabasının momentumu (yatay): M \cdot v_2
    • Cisim in momentumu:
      • Yatay bileşen: m \, v \,\cos\alpha
      • Düşey bileşen: m \, v \,\sin\alpha

Dolayısıyla çarpışma sonunda, X arabası + cisim birlikte hareket eder. Toplam kütle (M + m) olup, toplam momentumun hem yatay hem de düşey bileşeni korunur. Sonuçta nihai hızın büyüklüğü v'_x şu şekilde bulunur:

|\vec{p}_{\text{son}}| = \sqrt{\bigl(M v_2 + m v \cos \alpha \bigr)^2 + \bigl(m v \sin \alpha \bigr)^2}

Ardından hız:

v'_x = \frac{|\vec{p}_{\text{son}}|}{M + m} = \frac{\sqrt{\left(M v_2 + m v \cos \alpha\right)^2 + \left(m v \sin \alpha\right)^2}}{M + m}.

4. Şekil II (Y Arabası) – Düşey Çarpışma

Şekil II’de Y arabası yatayda v_2 hızıyla ilerlerken, çarpan cisim bu sefer ağırlıklı olarak düşey doğrultuda (örneğin dikine aşağı) hız v ile gelir. Böylece ilk toplam momentumun bileşenleri:

  • Yatay: M \, v_2
  • Düşey: m \, v

Bu durumda çarpışma sonrasında (çarpışan iki kütle birbirine yapıştığı anda), sistemin toplam momentumu:

|\vec{p}_{\text{son}}| = \sqrt{(M v_2)^2 + (m v)^2}.

Toplam kütle yine (M + m) olduğundan, Y arabasının son hızı v'_y şu olur:

v'_y = \frac{\sqrt{(M v_2)^2 + (m v)^2}}{M + m}.

5. Şekil III (Z Arabası) – Yatay Çarpışma

Şekil III’de ise Z arabası, v_2 yatay hızıyla giderken, cisim de (örneğin yatay doğrultuda) v büyüklüğünde hızla çarpmaktadır. Burada, çarpan cismin tamamen yatay bileşenli bir momentuma sahip olduğunu düşünürsek, toplam momentum:

  • Yatay: M \, v_2 + m \, v
  • Düşey: 0

Dolayısıyla son momentum:

|\vec{p}_{\text{son}}| = (M v_2 + m v)

ve bunun kütle (M + m) ile bölünmesi, son hız $v’_z$’yi verir:

v'_z = \frac{M v_2 + m v}{M + m}.

6. Son Hızların Birbirleriyle Karşılaştırılması

Yukarıdaki büyüklükleri tek tek incelersek:

  1. v'_z (Şekil III) genelde en büyük değer çıkar. Çünkü hem araba hem cisim aynı yönde yatay bileşenle çarpışırlar, momentumu maksimum yatay katkı sağlanarak büyütürler.
  2. v'_x (Şekil I) ise bu ikisinin arasında kalır. Bu durumda cisim, bir miktar yatay bileşen (pozitif yönde) ve bir miktar düşey bileşen katmaktadır. Dolayısıyla yatay bileşen m v \cos \alpha, dikey bileşen m v \sin \alpha ile birleşerek, toplam vektörsel hız v'_x orta düzeyde gerçekleşir.
  3. v'_y (Şekil II) en küçük çıkma eğilimindedir, çünkü cisim tüm hızıyla düşey doğrultuda gelmekte ve yatayda aynı yöne ek hız kazandırmadığı için, son hızın büyüklüğü ötekilerden düşük olur.

Matematiksel olarak, şu eşitsizlik doğrulanır:

v'_z > v'_x > v'_y .

Böylece “III numaralı şekildeki Z arabasının son hızı en büyük, II numaralı şekildeki Y arabasının son hızı en küçük, I numaralı şekildeki X arabasınınki ise arada” yorumunu yapabiliriz.

7. Özet Tablo

Aşağıdaki tabloda her şekil için çarpışma sonrası toplam momentumu ve son hızı gösterilmektedir:

Şekil Yatay Ön Momentum Düşey Ön Momentum Son Momentum Son Hız Büyüklüğü
I (X) M v_2 + m v \cos \alpha m v \sin \alpha \sqrt{\bigl(M v_2 + m v \cos \alpha \bigr)^2 + (m v \sin \alpha)^2} \dfrac{\sqrt{(M v_2 + m v \cos \alpha)^2 + (m v \sin \alpha)^2}}{M + m}
II (Y) M v_2 m v \sqrt{(M v_2)^2 + (m v)^2} \dfrac{\sqrt{(M v_2)^2 + (m v)^2}}{M + m}
III (Z) M v_2 + m v 0 (M v_2 + m v) \dfrac{M v_2 + m v}{M + m}

Tablodan görüldüğü gibi III. şekil (Z arabası) yatay momentumu en fazla şekilde artırdığı için son hız değeri en büyük, II. şekil (Y arabası) ise cisim dikeyden geldiği için yatay bileşene ekleme yapamadığı için en küçük kalır.

Sonuç:
Yukarıdaki analiz ve momentum korunumuna dayalı hesaplar ışığında, üç araba arasındaki çarpışma sonrası hız ilişkisi:

v'_z > v'_x > v'_y

şeklinde ifade edilebilir.

Teşekkürler @Haleeeess