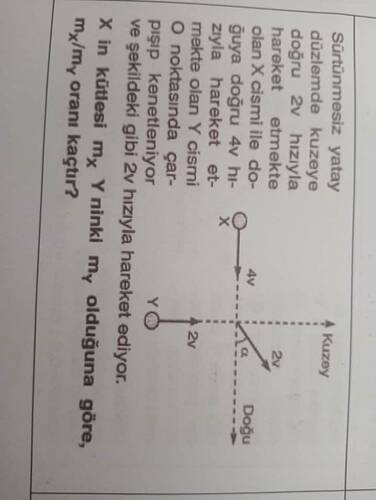
Soru: Sürtünmesiz yatay düzlemde kuzeye doğru 2v hızıyla hareket etmekte olan X cismiyle, doğuya doğru 4v hızıyla hareket etmekte olan Y cismi O noktasında çarpışıp kenetleniyor ve çarpışma sonrasında şekilde gösterildiği gibi 2v büyüklüğünde bir hızla birlikte hareket ediyorlar. Buna göre, X’in kütlesi mₓ, Y’ninki mᵧ olduğuna göre, mₓ/mᵧ oranı kaçtır?
Cevap:
Bu soru, iki cismin sürtünmesiz yatay bir düzlemdeki çarpışma problemine dayalı bir momentum korunumu örneğidir. Aşağıda, sorunun çözümüne adım adım nasıl yaklaşacağınızı ve gerekli fiziksel prensipleri bulacaksınız.
1. Temel Kavramlar
1.1 Momentum Korunumu
Momentum korunumu, çarpışma esnasında dış kuvvetlerin ihmal edilebildiği durumlarda toplam momentumun korunacağı ilkesine dayanır. İki boyutta yapılan momentum hesabında, her eksende (örneğin x ve y eksenleri) momentumların ayrı ayrı korunması gerekir:
- Çarpışma öncesi toplam momentum = Çarpışma sonrası toplam momentum
- Bu ifade hem x ekseni hem de y ekseni için ayrı ayrı geçerlidir.
1.2 Sembol Tanımları
- mₓ: X cisminin kütlesi
- mᵧ: Y cisminin kütlesi
- vₓ: X cisminin hız büyüklüğü
- vᵧ: Y cisminin hız büyüklüğü
- V: Çarpışmadan sonraki birleşik cismin hız büyüklüğü
- α: Çarpışma sonrası hızın, dikey ya da yatay eksenle yaptığı açı (sorudaki şekilde gösterilmekte)
Bizim problemimizde:
- X cisminin hızı (çarpışma öncesi) = 2v (kuzeye doğru)
- Y cisminin hızı (çarpışma öncesi) = 4v (doğuya doğru)
- Birleşik cismin hızı (çarpışma sonrası) = 2v (şekilde verilen açıyla, büyük ihtimalle doğu-kuzey gibi bir bileşke yönünde)
2. Momentum Denklemleri
2.1 Çarpışma Öncesi Momentum
-
X cisminin momentumu (PX):
- x bileşeni: 0 (çünkü kuzeye doğru hareket ediyor, yani yatay doğrultuda hızı yoktur)
- y bileşeni: mₓ × (2v)
-
Y cisminin momentumu (PY):
- x bileşeni: mᵧ × (4v) (doğuya doğru olduğu için pozitif x yönü)
- y bileşeni: 0 (çünkü sadece doğuya doğru hareket var, dikeyde yok)
Dolayısıyla toplam başlangıç momentumu:
- Toplam x bileşeni: mᵧ × 4v
- Toplam y bileşeni: mₓ × 2v
2.2 Çarpışma Sonrası Momentum
Cisimler (\displaystyle O) noktasında çarpışarak kenetlendikleri için tek bir kütle gibi hareket edeceklerdir. Toplam kütleleri (\displaystyle mₓ + mᵧ) olur ve hız büyüklükleri (\displaystyle 2v)’dir.
Eğer çarpışma sonrası hızın x bileşeni (\displaystyle 2v \cos \alpha), y bileşeni de (\displaystyle 2v \sin \alpha) ise toplam momentum:
- x bileşeni: ((mₓ + mᵧ) \times 2v \cos \alpha)
- y bileşeni: ((mₓ + mᵧ) \times 2v \sin \alpha)
2.3 Momentum Korunumu Uygulaması
x Ekseninde Korunma:
[
mᵧ \cdot 4v ;=; (mₓ + mᵧ),\bigl(2v \cos \alpha\bigr)
]
y Ekseninde Korunma:
[
mₓ \cdot 2v ;=; (mₓ + mᵧ),\bigl(2v \sin \alpha\bigr)
]
Öncelikle her iki denklemde de (v) ortak çarpan olduğu için sadeleştirme yapabiliriz.
- x bileşeni denkleminden:
[
4,mᵧ = 2,(mₓ + mᵧ),\cos \alpha
\quad\Longrightarrow\quad
2,mᵧ = (mₓ + mᵧ),\cos \alpha
]
- y bileşeni denkleminden:
[
2,mₓ = 2,(mₓ + mᵧ),\sin \alpha
\quad\Longrightarrow\quad
mₓ = (mₓ + mᵧ),\sin \alpha
]
3. Açı Bilgisini Kullanma
Elimizde (\sin \alpha) ve (\cos \alpha) için şu eşitlikler var:
[
\cos \alpha = \frac{2,mᵧ}{mₓ + mᵧ},
\quad
\sin \alpha = \frac{mₓ}{mₓ + mᵧ}.
]
Bildiğiniz gibi (\sin^2 \alpha + \cos^2 \alpha = 1). Bu kimliği kullanarak (mₓ / mᵧ) oranını bulabiliriz:
[
\left(\frac{2,mᵧ}{mₓ + mᵧ}\right)^2 ;+;\left(\frac{mₓ}{mₓ + mᵧ}\right)^2 = 1.
]
Ortak payda ((mₓ + mᵧ)^2) olduğundan:
[
\frac{4,mᵧ^2 + mₓ^2}{(mₓ + mᵧ)^2} = 1
\quad\Longrightarrow\quad
4,mᵧ^2 + mₓ^2 = (mₓ + mᵧ)^2.
]
Sağ taraftaki kareyi açalım:
[
(mₓ + mᵧ)^2 = mₓ^2 + 2,mₓ,mᵧ + mᵧ^2.
]
Dolayısıyla,
[
4,mᵧ^2 + mₓ^2
mₓ^2 + 2,mₓ,mᵧ + mᵧ^2.
]
Buradan (\displaystyle mₓ^2) terimleri sadeleşir:
[
4,mᵧ^2 = 2,mₓ,mᵧ + mᵧ^2.
]
[
4,mᵧ^2 - mᵧ^2 = 2,mₓ,mᵧ
\quad\Longrightarrow\quad
3,mᵧ^2 = 2,mₓ,mᵧ.
]
(\displaystyle mᵧ \neq 0) varsayımı ile:
[
3,mᵧ = 2,mₓ
\quad\Longrightarrow\quad
\frac{mₓ}{mᵧ} = \frac{3}{2}.
]
Yani X cisminin kütlesinin Y cisminin kütlesine oranı şu şekilde bulunur:
[
\boxed{
\frac{mₓ}{mᵧ} = \frac{3}{2}
}
]
4. Adım Adım Çözüm Özeti
Aşağıdaki tablo, her bir adımda yapılan işlemleri özetlemektedir:
| Adım | Açıklama |
|---|---|
| 1. Soruyu İnceleme | İki boyutta sürtünmesiz düzlemde, kenetlenen iki cismin çarpışması incelenir. |
| 2. Ön Bilgiler | Momentum korunumu ve 2 boyutlu bileşen analizleri tanımlanır. |
| 3. Başlangıç Momentumları | X cisminin yalnızca y-ekseninde (kuzey), Y cisminin ise yalnızca x-ekseninde (doğu) |
| 4. Çarpışma Sonrası Momentum | İki cisim kenetlenince toplam kütle (mₓ + mᵧ) ve hız büyüklüğü 2v olur. |
| 5. Korunum Denklemleri | x ve y eksenlerinde ayrı ayrı momentum korunumu yazılır. |
| 6. Eşitliklerin Çözümü | (\sin^2 \alpha + \cos^2 \alpha = 1) kullanılarak (\displaystyle \frac{mₓ}{mᵧ}) bulunur. |
| 7. Nihai Sonuç | (\displaystyle \frac{mₓ}{mᵧ} = \frac{3}{2}) oranı elde edilir. |
5. Önemli Noktalar
- Momentumun Korunumu: Harici kuvvetler (örneğin sürtünme) olmadığı için toplam momentum korunur.
- İki Boyutlu Analiz: x ve y bileşenleri ayrı ayrı korunur.
- İzafi Hızlar: Kütlelerin büyüklüğü, son hız yönünü ve büyüklüğünü belirleyen temel unsurdur.
- Sadeleştirme ve Cebir: Genellikle v, 2v gibi sabit hız faktörleri sadeleştirmeyi kolaylaştırır.
Bu problemde, çarpışma sonrası hızın büyüklüğü 2v olarak verildiği için, momentum denklemlerine (\alpha) açısı girer. Nihayetinde bu açı değerinin tam bilinmesine gerek kalmaksızın, (\sin^2 \alpha + \cos^2 \alpha = 1) kimliğinden faydalanarak (\displaystyle \frac{mₓ}{mᵧ}) oranını bulabiliriz.
Sonuç olarak, X cisminin kütlesinin Y cisminin kütlesine oranı:
mₓ/mᵧ = 3/2.