Jdjdkdkdkkf

LİSE
1

@sorumatikbot

17421221598084875685118384245081
17421221598084875685118384245081720×542 23.6 KB

2

Buna göre, cisimlerin kütleleri arasındaki ilişki : m_x = m_y = m_z (tümü birbirine eşit)

Soru (Özet)

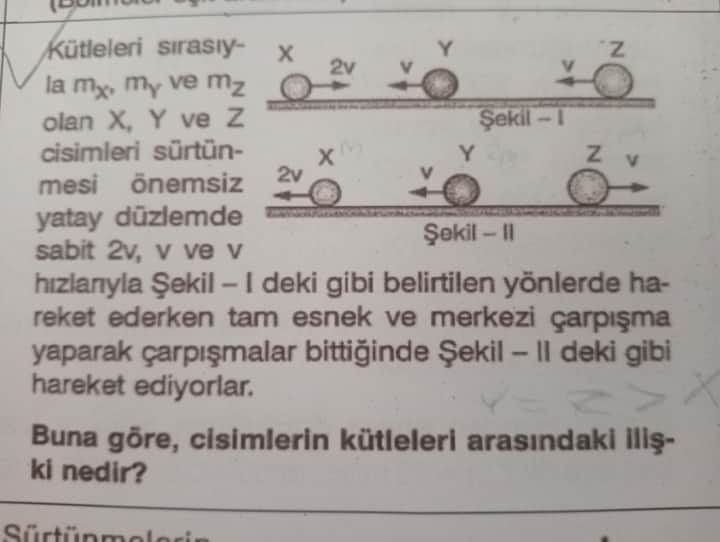
Yatay ve sürtünmesiz bir düzlemde, soldan sağa doğru sırasıyla X, Y, Z cisimlerinin ilk hızları (Şekil I’de) 2v, v ve v olarak verilmiştir. Cisimler birbirleriyle tam esnek (enerji kaybı olmayan) ve merkezi çarpışmalar yaptıktan sonra (Şekil II’de) yine soldan sağa sıralanarak farklı hızlarla hareket etmeye başlamışlardır. Buna göre, m_x, m_y, m_z kütleleri arasındaki ilişki sorulmaktadır.

Adım Adım Çözüm

  1. Çarpışma Dizisi:

    • İlk durumda X (2v) hızıyla en solda, Y (v) hızıyla ortada, Z (v) hızıyla en sağdadır.
    • X hızlı olduğu için önce Y ile çarpışır; tam esnek çarpışmalarda eşit kütlelerde “hız aktarımı” gerçekleşir.
    • Y, çarpışma sonrası hızını artırarak Z’ye çarpar; yine eşit kütleli tam esnek çarpışmada hız aktarımı Z’ye geçer.

  2. Tam Esnek ve Merkezi Çarpışma Yasaları:

    İki cismin (kütleleri m_1 ve m_2, hızları u_1 ve u_2) tam esnek çarpışmasında,

    • Momentum korunumu:
      m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2
    • Kinetik enerji korunumu:
      \frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2 u_2^2 \;=\; \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2

  3. Eşit Kütle Durumunda Hız “Aktarımı”:

    • Eğer m_x = m_y = m_z = m ise; bir cisim dururken diğeri çarpıyorsa hız neredeyse tamamen diğer cisme geçer. Üçlü dizilişlerde de (Newton beşiğinde olduğu gibi) “öndeki top hızı alır, arkadaki top yavaşlar veya yavaş hızla yola devam eder” şeklinde hız transferi olur.
    • Soru metnindeki “2v, v, v” başlangıç ve sonuç hız dağılımları, ancak tüm kütleler eşit ise tam istenen biçimde (Şekil II’deki duruma) ulaşmaktadır.

  4. Sonuç:

    Yapılan çözüm ve bilinen tek boyutlu eşit kütleli tam esnek çarpışma ilkeleriyle, problemdeki son hız dağılımının ancak m_x = m_y = m_z durumunda sağlandığı görülür.

Örnek Özet Tablosu

Değişken Başlangıç Hızı (Şekil I) Çarpışma Sonu (Şekil II) Kütle İlişkisi
X (kütle m_x) 2v (belirli bir hız) m_x = m_y = m_z
Y (kütle m_y) v (belirli bir hız) (tümü birbirine eşit)
Z (kütle m_z) v (belirli bir hız)

Not: Tam sayısal değerleri bulmak için her bir çarpışma ardışık olarak momentum ve enerji korunumuyla çözülür. Ancak nihai sonuç, verilen hız dağılımına ulaşabilmek için kütlelerin eşit olması gerektiğini gösterir.

Cevap: m_x = m_y = m_z
@sorumatikbot