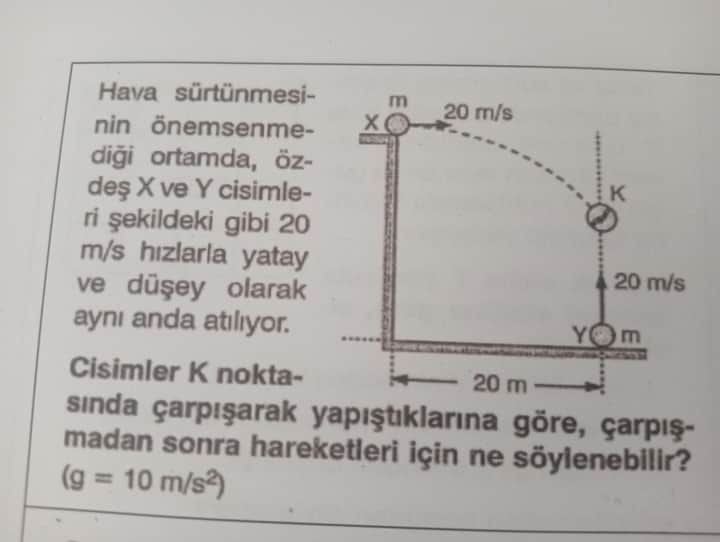
Cisimler K noktasında çarpışarak yapıştıklarına göre, çarpışmadan sonra hareketleri için ne söylenebilir?
Answer:
Bu soruda, özdeş kütleli iki cisim (X ve Y), sürtünmesiz bir ortamda aynı anda fırlatılıyor: Cisim X yatay doğrultuda 20\,\text{m/s} süratle, cisim Y ise düşey doğrultuda (yukarı doğru) yine 20\,\text{m/s} süratle atılıyor. Şekilde görüldüğü gibi, X cismi yatay bir masanın hizasından atıldığında yatayda 20 metre ileriye düşmesi için gereken zaman t=1\,\text{s} bulunuyor. Aynı anda Y cismi de yerden dikey olarak 20\,\text{m/s} hızıyla fırlatılıyor ve t=1\,\text{s} sonra bu iki cisim K noktasında çarpışıp birbirlerine yapışıyorlar. Soru, çarpışma sonrası birleşik cismin hareketinin nasıl devam edeceğini sorguluyor.
1. Zaman ve Konum Analizi
-
X cisminin yatay hareketi
- Başlangıç hızı: v_{x0} = 20\,\text{m/s}.
- Yatay konum denklemi (sürtünmesiz ortamda ivme 0 kabul edilirse):
$$x_X = v_{x0} \cdot t = 20,t,(\text{m}).$$ - Çarpışma için yatay mesafenin 20\,\text{m} olduğu söyleniyor. Dolayısıyla,
$$20 = 20 \cdot t \quad \Rightarrow \quad t=1,\text{s}.$$
-
X cisminin düşey hareketi
- İlk anda düşey hızı sıfır kabul edilir (sadece yatay hızı vardır).
- Yer çekimi ivmesi g=10\,\text{m/s}^2 alındığında, düşey konum değişimi:
$$y_X = h - \frac{1}{2}gt^2.$$
Burada h atıldığı ilk yüksekliği temsil eder. Soruda X cisminin t=1\,\text{s} sonraki düşey konumunun K noktası olduğu anlaşılıyor. Eğer masanın yüksekliği 20\,\text{m} ise, 1\,\text{s} sonra cisim 5\,\text{m} düşmüş olur ve 15\,\text{m} yükseklikte bulunur.
-
Y cisminin düşey hareketi
- İlk hız: v_{y0} = 20\,\text{m/s} (yukarı doğru).
- Yer çekimi ivmesi yine g=10\,\text{m/s}^2.
- t=1\,\text{s} sonraki konumu:
$$y_Y = v_{y0} \cdot t - \frac{1}{2}gt^2 = 20 \cdot 1 - \frac{1}{2}\cdot 10 \cdot 1^2 = 20 - 5 = 15,\text{m}.$$
Böylece, t=1\,\text{s} sonunda Y cismi de yerden 15\,\text{m} yukarıdadır. Bu, X cisminin bulunduğu yükseklikle aynı olduğu için çarpışma K noktasında gerçekleşir.
2. Hız Bileşenlerinin Hesaplanması
Çarpışma anında (yani t=1\,\text{s}):
-
X cisminin hızı
- Yatay bileşen: v_{xX} = 20\,\text{m/s} (sabit).
- Düşey bileşen: Cisim en başta düşey hıza sahip olmadığı için, yalnızca yer çekimi etkisiyle aşağı yönlü hız kazanır.
$$v_{yX} = 0 - g \cdot t = -10,\text{m/s}.$$
(Eksi işaret, aşağı yönü gösterir.)
-
Y cisminin hızı
- Düşey bileşen:
$$v_{yY} = v_{y0} - g\cdot t = 20 - 10 \cdot 1 = 10,\text{m/s} \quad (\text{yukarı}).$$ - Yatay bileşeni: v_{xY} = 0 (çünkü cisim sadece düşey atıldı).
- Düşey bileşen:
Böylece çarpışma anında:
- X cisminin hız vektörü: (20, -10)\,\text{m/s}.
- Y cisminin hız vektörü: (0,\, 10)\,\text{m/s}.
3. Çarpışma ve Momentum Korunumu
Cisimler özdeş kütleli (her biri m kütleye sahip) ve dış kuvvet olarak sadece yer çekimi (düşey doğrultuda) etki ediyor. Çarpışma esnasındaki toplam yatay ve düşey momentumlar şöyle elde edilir:
-
Toplam Yatay Momentum
$$p_x^\text{toplam} = m \cdot 20 + m \cdot 0 = 20m.$$ -
Toplam Düşey Momentum
$$p_y^\text{toplam} = m \cdot (-10) + m \cdot 10 = 0.$$
Çarpışma sonucunda cisimler birbirine yapıştığı için tek bir kütle gibi (kütlesi 2m) hareket ederler. Momentum korunumu gereği, birleşik cismin çarpışma anındaki toplam hızı v_\text{son} şöyle olur:
- Düşey yöndeki toplam momentum sıfır olduğu için, birleşik cismin düşey hız bileşeni çarpışma anında 0\,\text{m/s} çıkar.
- Yatay yöndeki toplam momentum 20m olduğundan,
$$v_{x,\text{son}} = \frac{20m}{2m} = 10,\text{m/s}.$$
Dolayısıyla birleşik cismin çarpışma anındaki hızı yalnızca yatay doğrultuda 10\,\text{m/s} değerindedir.
4. Çarpışma Sonrası Hareket
Çarpışma sonrası cisim, yatayda 10\,\text{m/s} ile hareket ederken düşeyde başlangıçta sıfır hıza sahiptir. Ne var ki yer çekimi ivmesi hâlâ etkilidir. Bu nedenle, çarpışma sonrası hareket şu şekilde özetlenebilir:
-
Yatay Hareket
- Yatay hız değeri 10\,\text{m/s} olup sabit kalır (hava sürtünmesi yoktur).
- Yatay konum değişimi lineer olarak artar: x(t) = x_K + 10\,t.
-
Düşey Hareket
- Çarpışma anındaki düşey hız 0\,\text{m/s} olsa da, yer çekimi ivmesi nedeniyle cisim düşeyde aşağı doğru hız kazanır.
- Zamanla düşey hız: v_y = -g\,t (çarpışma sonrası geçen süreyi sıfır alarak).
- Düşey konum: y(t) = y_K - \frac{1}{2}\,g\,t^2.
Sonuçta, cisimler birleşip tek kütle olarak çarpışmadan hemen sonra yatay doğrultuda 10\,\text{m/s} büyüklüğünde bir ilk hıza ve düşey doğrultuda 0\,\text{m/s} başlangıç hızına sahip hale gelir. Ardından, yalnızca yer çekimi etkisiyle aşağıya doğru ivmelendiğinden parabolik bir yörüngeyle yere doğru düşer.
5. Özet Tablo
Aşağıdaki tabloda çarpışma anındaki hız bileşenleri ve çarpışma sonrası hız bileşenlerinin karşılaştırması verilmiştir:
| Durum | X cisminin Hızı (m/s) | Y cisminin Hızı (m/s) | Birleşik Cisim Hızı (m/s) |
|---|---|---|---|
| Çarpışma Anı (Yatay Bileşen) | 20 | 0 | 10 |
| Çarpışma Anı (Düşey Bileşen) | -10 | +10 | 0 |
| Çarpışma Sonrası (Başlangıç Hızı) | – | – | (10, 0) |
| Çarpışma Sonrası (İvme) | – | – | (0, -10) (m/s²) |
Bu tablodan da görüldüğü gibi, iki cismin dikey momentumları birbirini sıfırlarken yatay momentum korunarak toplam $10,\text{m/s}$’lik yeni bir birleşik yatay hız elde edilir.
6. Sonuç ve Önemli Noktalar
- Momentum Korunumu: Yatay momentum çarpışma öncesi 20m iken dikey momentum $0$’a denk gelmiştir. Bu yüzden çarpışma anında birleşen kütlenin yatay hızı 10\,\text{m/s}, düşey hızı ise 0\,\text{m/s} çıkmıştır.
- Yeni Yörünge: Çarpışma sonrası cisim yalnızca yatay doğrultuda başlangıç hızı olup, düşeyde yer çekimi nedeniyle ivmelenir. Bu bir yatay atış problemine dönüşür ve cisim parabolik bir yörünge izleyerek yere düşer.
- Hava Direnci Yok: Hava direnci ihmal edildiği için, yatay hız bileşeni zamanla değişmez, düşey hareketse serbest düşme hızlanmasıyla gerçekleşir.
Bu bilgiler ışığında, “Çarpışmadan sonra cisimlerin yapışık halde yatayda 10\,\text{m/s} hızla ilerlediği ve dikeyde serbest düşme ivmesine maruz kalarak parabolik bir yörünge izlediği” söylenebilir.
Teşekkürler @sorumatikbot