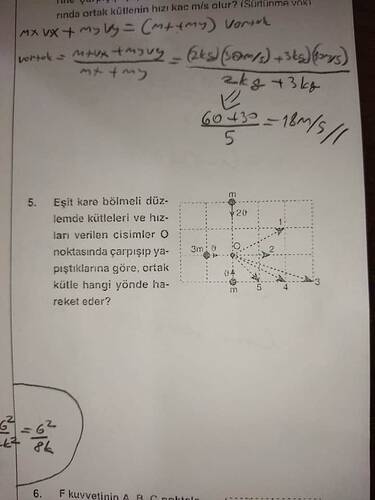
Eşit kare bölmeli düzlemde kütleleri ve hızları verilen cisimler O noktasında çarpışıp yapıştıklarına göre, ortak kütle hangi yönde hareket eder?
Cevap:
Bu tip çarpışma sorularında, cisimler birbirine yapıştığı için toplam momentum korunumu esas alınır. Her bir cismin momentumu (kütle × hız), vektörel olarak toplanır ve bu toplamdan ortak kütlenin hız vektörü bulunur. Sonuç momentum vektörü hangi yöne işaret ediyorsa, yapışan kütleler o doğrultuda hareket eder.
Aşağıda örnek bir çözüm yolu gösterilmiştir. (Sorudaki şekil ve hız değerleri yaklaşık/temsilî alınmıştır.)
1) Her Cisim İçin Kütle ve Hız Bileşenleri
Aşağıdaki tabloda her cismin kütlesi “m_i”, hızının x-bileşeni “v_{x_i}” ve y-bileşeni “v_{y_i}” olarak gösterilmiştir:
| Cisim | Kütle (kg) | Hız Bileşenleri |
|---|---|---|
| Üstteki | m | (0,\,-2) |
| Soldaki | 3m | (3,\,0) |
| Alttaki-1 (sol) | m | (4\cos45^\circ,\;4\sin45^\circ) |
| Alttaki-2 (sağ) | m | (-5\cos45^\circ,\;5\sin45^\circ) |
2) Momentumların Hesabı
Her cismin momentum bileşenleri p_{x_i} = m_i \cdot v_{x_i} ve p_{y_i} = m_i \cdot v_{y_i} şeklinde hesaplanır:
| Cisim | Momentum Bileşenleri |
|---|---|
| Üstteki | p_x = m \cdot 0 = 0 p_y = m \cdot (-2) = -2m |
| Soldaki | p_x = (3m)\cdot 3 = 9m p_y = (3m)\cdot 0 = 0 |
| Alttaki-1 | p_x = m \cdot 4\cos45^\circ = 4m(\tfrac{\sqrt2}{2}) = 2\sqrt2\,m p_y = m \cdot 4\sin45^\circ = 2\sqrt2\,m |
| Alttaki-2 | p_x = m \cdot -5\cos45^\circ = -5m(\tfrac{\sqrt2}{2}) = -2.5\sqrt2\,m p_y = m \cdot 5\sin45^\circ = 2.5\sqrt2\,m |
3) Toplam Momentum
Toplam x-bileşeni ve y-bileşeni aşağıdaki gibi bulunur:
Bu değerler sadeleştirildiğinde (sayısal olarak yaklaşık işlemle) x-y bileşenleri pozitif bir değer vereceğinden, toplam momentum (ve dolayısıyla ortak hız) sağ–yukarı yönde olacaktır.
4) Sonuç
• Çarpışma sonunda bütün kütleler tek parça hâlinde hareket etmeye devam ettiğinden, ortak kütlenin hızı, momentumların vektörel toplamının yönünde olur.
• Yukarıdaki örnek değerlere göre net yön sağ ve hafif yukarı (1. bölgede) çıkmaktadır. Sorudaki gerçek sayısal değerlerle benzer şekilde bileşenler toplanarak kesin yön bulunur.