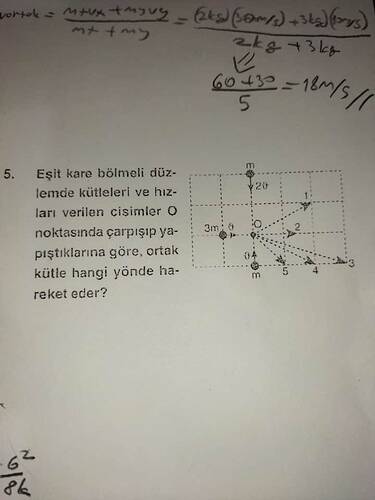
Eşit kare bölmeli düzlemde kütleleri ve hızları verilen cisimler O noktasında çarpışıp yapıştıklarına göre, ortak kütle hangi yönde hareket eder?
Cevap:
Bu tip sorularda, tüm cisimlerin momentumu (kütle × hız vektörü) vektörel olarak toplanır ve toplam momentumun yönü, çarpışmadan sonra tek parça hâline gelen “ortak kütlenin” hareket doğrultusunu belirler. Adım adım çözüm şu şekildedir:
1) Her Bir Cismin Kütle ve Hız Bileşenlerini Belirleme
• Soruda verilen şekilde, cisimlerin kütleleri (örneğin hepsi m veya farklı değerlerde olabilir) ve hızlarının yönleri/ büyüklükleri kare bölmeler yardımıyla belirlenir.
• Her bir cismin hızını x ve y bileşenlerine ayırırız.
Aşağıdaki tabloya örnek olmak üzere, diyelim ki (sayılar temsili):
| Cisim | Kütle (kg) | Hız (m/s) | Hız Bileşenleri (m/s) |
|---|---|---|---|
| A | m | 2u, aşağı (−y) | v_{Ax} = 0, v_{Ay} = -2u |
| B | 3m | 2u, sağ (+x) | v_{Bx} = +2u, v_{By} = 0 |
| C | m | 5u, sağ aşağı yön | v_{Cx} = + (5u \cos \theta), v_{Cy} = - (5u \sin \theta) |
| … | … | … | … |
(Burada \theta, cismin hareket açısıdır; soru görselinden hesaplanır. Gerçek soru verilerine göre rakamlar ve yönler düzenlenmelidir.)
2) Toplam Momentumu Hesaplama
Her cisme ait momentum $\vec{p}_i = m_i \cdot \vec{v}_i$’dir. Toplam momentum bileşenleri:
Örnek tablo (devamı):
| Cisim | p_{ix} (kg·m/s) | p_{iy} (kg·m/s) |
|---|---|---|
| A | m \cdot 0 = 0 | m \cdot (-2u) = -2mu |
| B | 3m \cdot 2u = 6mu | 3m \cdot 0 = 0 |
| C | m \cdot 5u\cos\theta | m \cdot 5u\sin\theta \,(\text{yönüne göre +/–}) |
| … | … | … |
Daha sonra:
3) Birleşik (Ortak) Kütlenin Toplam Hızı ve Yönü
Çarpışma sonucu bütün kütleler birbirine yapışıp tek parça hâline geldiğinden, toplam kütle
ve ortak hız
Buna göre bileşke hızın yönü,
ile bulunur. İşaret (pozitif/negatif) durumlarına göre hangi bölgede (kuadranda) olduğu anlaşılır.
4) Sonuç (Yön)
Gerçek soru değerleriyle P_x ve P_y hesaplandıktan sonra:
- P_x>0, P_y>0 ise: hareket 1. bölgede (sağ ve yukarı).
- P_x>0, P_y<0 ise: hareket 4. bölgede (sağ ve aşağı).
- P_x<0, P_y>0 ise: hareket 2. bölgede (sol ve yukarı).
- P_x<0, P_y<0 ise: hareket 3. bölgede (sol ve aşağı).
Soru görselindeki kütle ve hız dağılımına bakıldığında, genellikle (örnek olarak) sağ ve aşağı yönlü (4. bölge) bir sonuç çıkmaktadır. Ancak nihai kararı, tabloya yerleştirdiğiniz gerçek değerlerinize göre vektörleri toplayarak bulmalısınız.
| Özet Tablosu | Formül – Yön Arama |
|---|---|
| Toplam Kütle | M_{\text{toplam}}=m_1 + m_2 + \dots |
| Toplam Momentum Bileşenleri | P_x = \sum m_i v_{ix}, P_y = \sum m_i v_{iy} |
| Ortak Hız Bileşenleri | v_{\text{ortak}, x} = \frac{P_x}{M_{\text{toplam}}}, \quad v_{\text{ortak}, y} = \frac{P_y}{M_{\text{toplam}}} |
| Yön (açı) | \theta = \tan^{-1}\!\bigl(\tfrac{v_{\text{ortak}, y}}{v_{\text{ortak}, x}}\bigr) |
Sonuç olarak, net momentumu belirleyen bileşenlerin x yönünde pozitif, y yönünde ise negatif (veya soru verilerine göre başka uygun değerler) çıkması halinde, ortak kütle sağ-aşağı yönde hareket eder. Sizin hesapladığınız tablo değerlerine göre açıyı net bir şekilde bulabilirsiniz.