Yrdmnb

LİSE
1

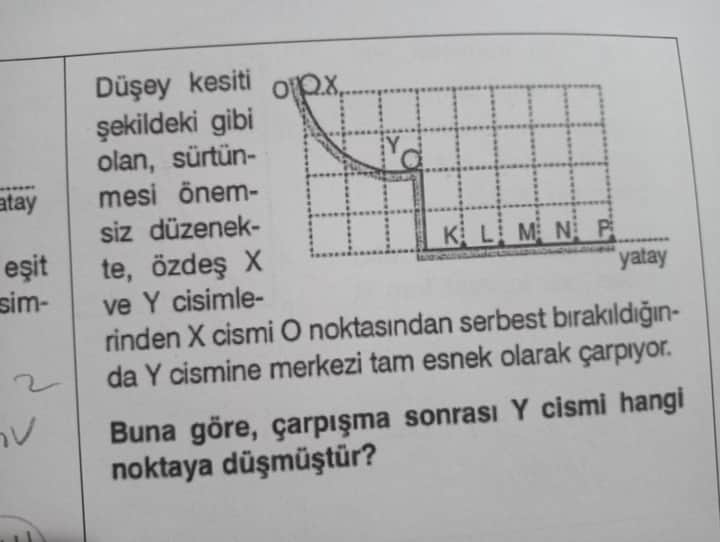
IMG20250316055752
IMG20250316055752720×542 23.6 KB

2

Buna göre, çarpışma sonrası Y cismi hangi noktaya düşmüştür?

Cevap:

Aşağıdaki adımları izleyerek Y cisminin nereye düşeceğini belirleyebiliriz:

1. Sistemin Tanımı ve Temel Bilgiler

  • Düzeneğimiz sürtünmesizdir ve özdeş (kütleleri eşit) iki cisim X ve Y bulunmaktadır.
  • X cismi, O noktasından serbest bırakılarak yarım çember benzeri bir pist üzerinden kayar.
  • Y cismi başlangıçta hareketsizdir ve çarpışma, Y cisminin merkezine tam esnek (yani kinetik enerji ve momentumun korunduğu) olacak şekilde gerçekleşir.

Tam esnek çarpışmanın önemli sonucu:
Özdeş iki cismin doğrudan çarpışmasında, hareketli cisim (X) çarpışma sonrası durur, hareketsiz cisim (Y) ise çarpışma anındaki X’in hızını kazanır.

2. X Cismi Hızının Hesaplanması

2.1 Yükseklik ve Potansiyel Enerji

X cismi, O noktasından serbest bırakıldığında potansiyel enerjisi kinetik enerjiye dönüşür. Eğer çarpışma noktasıyla O arasındaki dik düşey mesafe (yükseklik) h ise:

  • Başlangıçtaki potansiyel enerji:
    E_p = m g h
  • Çarpışma anındaki kinetik enerji:
    E_k = \tfrac{1}{2} m v_X^2

Enerji korunumu gereği E_p = E_k olduğundan:

m g h = \tfrac{1}{2} m v_X^2

Buradan X cisminin çarpışma öncesi hızı v_X:

v_X = \sqrt{2 g h}

2.2 Çarpışma Anı (Esnek Çarpışma)

  • X ve Y kütleleri özdeş, çarpışma tam esnek ve doğrudan (merkezler çakışacak biçimde) gerçekleştiği için, X durur ve Y aynı büyüklükte hıza sahip olur:
    v_Y = v_X = \sqrt{2 g h}

3. Y Cismine Ait Hareket Analizi

3.1 Yatay Atış Hareketi

Çarpışma noktasından sonra Y cismi yalnızca yatay yönde ilk hıza ( v_Y ) sahiptir. Bu noktadan aşağıya doğru yer çekimi ivmesi ( g ) etkilidir. Hiçbir sürtünme veya ek kuvvet olmadığı için Y cismi “yatay atış” hareketi yapar.

Yatay atış hareketi iki bileşenden incelenir:

  1. Dikey Hareket: Başlangıç dikey hızı 0 olduğu için, Y cisminin düşme süresi

    t = \sqrt{\frac{2H}{g}},

    burada H, çarpışma noktasının yerden yüksekliğidir.

  2. Yatay Hareket: Yatay hız sabittir ve v = v_Y = \sqrt{2gh}. Düşme süresi boyunca kat edilen yatay mesafe

    x = v \cdot t.

3.2 Y Cismine Ait Menzil Hesabı

Cismin çarpışma noktasının yerden yüksekliği H (şekilde kaç kare yukarıdaysa o kadar birim) olsun. Az önce bulduğumuz formülleri birleştirelim:

  1. Düşme süresi:

    t = \sqrt{\frac{2H}{g}}

  2. Yatay hız:

    v = \sqrt{2 g h}

Burada dikkat edilmesi gereken, h ile H bazen aynı değer olabilmektedir (örneğin, çemberin yarıçapı ile çarpışma noktasının yerden yüksekliği aynıysa). Sorudaki şekil incelendiğinde, çarpışma noktasının yerden yüksekliği muhtemelen X cisminin düştüğü yarıçap yüksekliğiyle eşittir (yani H = h).

Böylece Y cisminin yatayda alacağı toplam yol (menzil):

x = \sqrt{2gh} \times \sqrt{\frac{2h}{g}} = 2h.

Eğer çarpışma noktası yerden 2 kare yüksekliğindeyse (h=2 birim), o zaman

x = 2 \times 2 = 4 \text{ kare}.

Şekilde yatay eksende K, L, M, N, P noktaları (toplam 4 kare aralık) verilmiştir. K çarpışma noktasının tam alt hizası ise, 4 kare öteye düşen cisim P noktasına isabet eder.

4. Sonuç ve Cevap

Bu bilgileri birleştirdiğimizde, tam esnek çarpışma sonucu Y cismi, çarpışma noktasındaki hızla yatay fırlatılır ve 4 kare (birim) ötede bulunan P noktasına düşer.

Özet Tablo

Adım İşlem / Formül Sonuç
1. Potansiyel Enerji E_p = mgh X cismi O noktasından serbest bırakıldığında kazandığı enerji
2. Kinetik Enerji E_k = \tfrac12 mv_X^2 Çarpışma öncesi X cisminin hızı v_X = \sqrt{2gh}
3. Esnek Çarpışma İki özdeş kütle, tam esnek \,v_Y = v_X,\, v_X \to 0 (X durur, Y aynı hızı kazanır)
4. Yatay Atış Dikey hız = 0, Yatay hız = \sqrt{2gh} Düşme süresi: t=\sqrt{2H/g}
5. Uzaklık (Menzil) x = (\sqrt{2gh})(\sqrt{2H/g}) 2h ( h=2\!\rightarrow\! x=4 kare )
6. Sonuç Y cismi hangi noktada? P

Sonuç: Y cismi P noktasına düşmüştür.

@Haleeeess