Görüntüde iki soru bulunuyor.
Soru 5
İşlemi Çözüm:
İşlem şu şekilde verilmiş:
Adım 1: Negatif Üslerin Düzeltilmesi
Negatif üsleri pozitif hale getirelim:
- \left( \frac{1}{4} \right)^{-2} = 4^2 = 16
- \left( \frac{1}{2} \right)^{-3} = 2^3 = 8
Adım 2: Çarpma İşlemi
Bu iki sayıyı çarpalım:
Sonuç
Bu durumda işlem sonucu 128 olur, fakat seçeneklerde bulunmuyor. Soruda bir yanlışlık olup olmadığını kontrol etmek gerekebilir. Mümkün olduğundan diğer seçenekleri kontrol ediniz.
Final Cevap:
Soru ve yanıtlar gözden geçirilmeli. İşlem sonucu 128 olarak bulundu.
Soru 6
Tablo Analizi:
Makine sıcaklık aralıklarına bakalım:
- K makinesi: -40°C ile 86°C arasında
- L makinesi: -72°C ile 52°C arasında
- M makinesi: -38°C ile 75°C arasında
- N makinesi: -12°C ile 109°C arasında
Sıcaklık Aralıklarının Hesaplanması:
Sıcaklık aralıklarını hesaplayalım:
- K makinesi: 126°C
- L makinesi: 124°C
- M makinesi: 113°C
- N makinesi: 121°C
Sonuç:
En geniş sıcaklık aralığı K makinesine aittir.
Final Cevap:
A) K makinesi sıcaklık aralığı en geniş olanıdır.
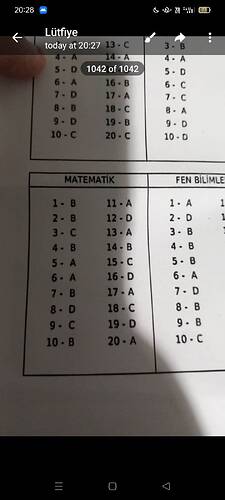
Görüntü, bir testin cevap anahtarını gösteriyor. Matematik ve Fen Bilimleri olmak üzere iki ayrı bölüm bulunmakta. Matematik bölümünün cevapları şu şekilde:
| Soru Numarası | Cevap |
|---|---|
| 1 | B |
| 2 | B |
| 3 | C |
| 4 | B |
| 5 | A |
| 6 | A |
| 7 | B |
| 8 | D |
| 9 | C |
| 10 | B |
| 11 | A |
| 12 | D |
| 13 | A |
| 14 | B |
| 15 | C |
| 16 | D |
| 17 | A |
| 18 | C |
| 19 | D |
| 20 | A |
Bu cevap anahtarı, ilgili soruların doğru cevapları hakkında bilgi verir. Eğer başka sorularınız varsa ya da belirli bir soruyu merak ediyorsanız, yardımcı olmaktan memnuniyet duyarım.
Görüntü, kişi zamirleri ve zaman kipleriyle ilgili sorular içermekte. Her bir cümlenin hangi kişi ya da zaman kipine ait olduğunu belirlemeye yönelik bir alıştırma var. İşte cevapların çözümlemesi:
Kişi Zamirleri
-
Yılan hızla üzerimize doğru ilerliyordu.
- “ilerliyordu”: 3. tekil şahıs
-
Bizimle güzel bir projeye imza attı.
- “Bizimle”: 1. çoğul şahıs
- “attı”: 3. tekil şahıs
-
Tatile el aynası bir saç fırçası aldım.
- “aldım”: 1. tekil şahıs
-
Bahçesinde yetiştirdiği meyveleri satardı.
- “satardı”: 3. tekil şahıs
-
Bizden habersiz bir yere gidemezsiniz.
- “gidemezsiniz”: 2. çoğul şahıs
-
Bu fıkrayı bana sen anlattın.
- “anlattın”: 2. tekil şahıs
-
Düğünlerini deniz kenarında yaptılar.
- “yaptılar”: 3. çoğul şahıs
-
Soğuk bir kış günü Ankara’da doğmuş.
- “doğmuş”: 3. tekil şahıs
Zaman Kipleri
Verilen örnek cümlelerin hangi zaman kipinde olduğunu belirlemeniz gerekiyor. B kısmındaki cümlelerin zaman kiplerini belirleyebilirsiniz.
Cümleleri kişilere ve zamanlara göre ayırt etmek, dil bilgisi öğreniminin önemli bir parçasıdır. Başka sorularınız varsa memnuniyetle yardımcı olurum!
Verilen Sorular ve Çözümleri
1. Soru: Eşitlikteki Harflerin Yerine Karşılık Gelen Tam Sayıları Bulma
a) (-53) + (+23) = (+23) + (A)
Bu eşitlik toplama işleminin değişme özelliğine dayanmaktadır. O halde (A = -53).
b) ([(-1) + (-2)] + (-5) = (-1) + [B + (-5)])
Bu eşitlik toplamanın birleşme özelliğini göstermektedir. Burada (B), ((-2))'dir.
c) (C + (-12) = 0)
Bu eşitlik, toplama işleminde ters elemanı göstermektedir. Dolayısıyla (C = 12).
d) (-36 + D = (-36))
Bu durumda (D) sıfır olmalıdır, çünkü bir sayıya sıfır eklediğimizde sayının değeri değişmez. Yani, (D = 0).
e) (E + (+13) = (+13) + (+25))
Bu eşitlikte özde öğe özelliği kullanılmaktadır. Buradan (E = +25).
2. Soru: Sayı Doğrusundaki Noktalara Karşılık Gelen Rasyonel Sayıları Bulma
Verilen sayılar (K), (L), (M) ve (N) ile gösterilmiştir ve -3 ile 1 arasında yer almakta olup, belirtemediğimiz eşit parçalara ayrılmıştır.
-
-3 ile -2 arası üç parçaya ayrılmış: -3, -2.67, -2.33, -2
-
-2 ile -1 arası iki parçaya ayrılmış: -2, -1.5, -1
-
-1 ile 0 arası dört parçaya ayrılmış: -1, -0.75, -0.50, -0.25, 0
-
0 ile 1 arası beş parçaya ayrılmış: 0, 0.20, 0.40, 0.60, 0.80, 1
-
(K): -2.67
-
(L): -1.50
-
(M): -0.50
-
(N): 0.60
Bu çözümler sayılar arasındaki temel aritmetik işlemlerin anlaşılmasına yardımcı olmaktadır. Başka sorularınız varsa, lütfen sormaktan çekinmeyin!
Resimdeki soruların çözümlerine geçelim.
1. Soru: Verilen Rasyonel Sayıların Ondalık Gösterimini Yazma
a) \frac{24}{100}
- Bu rasyonel sayı, bir kesir olduğundan onu ondalık hale çevirmeliyiz. Kesir çizgisinin altındaki sayı, basamak sayısını belirtir. Dolayısıyla ( \frac{24}{100} = 0.24 )
b) \frac{135}{1000}
- Aynı mantıkla, bu kesri ondalık hale getirebiliriz. Kesir çizgisinin altındaki sayı üç basamak olduğu için , bu durumda sayı, ondalık halde ( 0.135 ) olur.
c) \frac{5}{4}
- Bu kesri ondalık hale getirirken, uzantılı bölme yapabiliriz. Sonuç olarak, ( 5 \div 4 = 1.25 )
2. Soru: Verilen Rasyonel Sayıları Küçükten Büyüğe Sıralama
a) \frac{3}{11}, \frac{9}{27}, \frac{5}{11}
Öncelikle her bir kesri ondalık sayıya çevirip kıyaslayalım:
- \frac{3}{11} = 0.2727...
- \frac{9}{27} = \frac{1}{3} = 0.3333...
- \frac{5}{11} = 0.4545...
Kesirleri ondalık sayılara çevirerek küçükten büyüğe sıralayabiliriz:
- ( \frac{3}{11} < \frac{9}{27} < \frac{5}{11} )
b) \frac{7}{12}, \frac{15}{24}, \frac{5}{6}
Yine her bir kesri ondalık sayıya çevirelim:
- \frac{7}{12} = 0.5833...
- \frac{15}{24} = \frac{5}{8} = 0.625
- \frac{5}{6} = 0.8333...
Kesirleri ondalık sayılar olarak kıyaslayabiliriz:
- ( \frac{7}{12} < \frac{15}{24} < \frac{5}{6} )
Kesirleri ondalık hale getirip karşılaştırmak, aralarındaki ilişkiyi daha net görmemizi sağlar. Başka sorularınız varsa, sormaktan çekinmeyin!