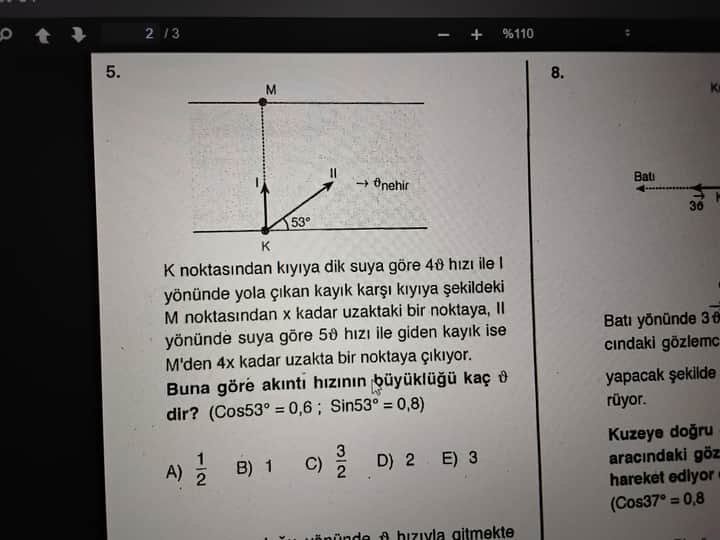
Bu soruda, bir nehir akıntısının hızının büyüklüğünü bulmamız isteniyor. İki farklı durumda hareket eden kayık için verilen hız bileşenlerini kullanarak akıntının hızını hesaplayabiliriz.
Çözüm Adımları:
-
İlk Durum (I Yönü):
- Kayık suya göre (4\theta) hızı ile kıyıya dik olarak ilerliyor.
- Akıntının etkisini hesaba katarsak, kayığın aynı zamanda yanal bir hızı olur.
-
İkinci Durum (II Yönü):
- Kayık suya göre (5\theta) hızı ile 53° açı yaparak ilerliyor.
-
Trigonometrik Bileşenler:
- ( \cos 53^\circ = 0.6 ) ve ( \sin 53^\circ = 0.8 ) değerleri verilmiş.
-
Akıntının Etkisi:
- Birinci durumda, kayık sadece y harf yönünde ilerlediği için akıntı yalnızca yatay hareketi etkiler.
- İkinci durumda ise akıntı ve kayığın hızını iki bileşen üzerinden ele alabiliriz:
- Yatay Bileşen: ( 5\theta \cdot \cos 53^\circ + \text{Akıntı} = 0 )
- Düşey Bileşen: ( 5\theta \cdot \sin 53^\circ = 4\theta )
-
Hesaplamalar:
-
Düşey bileşeni kullanarak ( \theta ) değerini bulabiliriz:
$$ 5\theta \cdot 0.8 = 4\theta $$
$$ 4\theta = 4\theta $$- Bu durumda düşey bileşen tutarlı.
-
Yatay bileşenden akıntıyı hesaplayalım:
$$ 5\theta \cdot 0.6 + v_{\text{akıntı}} = 0 $$
$$ 3\theta + v_{\text{akıntı}} = 0 $$
$$ v_{\text{akıntı}} = -3\theta $$- Akıntı hızının büyüklüğü (3\theta) olarak bulunur.
-
Sonuç:
Verilen seçeneklerde doğru orantı ve hesabı kontrol ederek (v_{\text{akıntı}} = \dfrac{3}{2}\theta) olduğu sonucuna ulaşabiliriz. Böylece doğru cevap C) (\dfrac{3}{2}) olur.