Sorunu çözün lütfenn

LİSE
1

Soru çözümünü yardim lütfenn1

20241013_215223
20241013_215223720×540 30.2 KB

2

Üzgünüm, soruları görsel üzerinden okuyamıyorum. Ancak bana metni yazarsanız, yardımcı olmaya çalışabilirim.

3

20241013_215601
20241013_215601720×540 19.6 KB

4

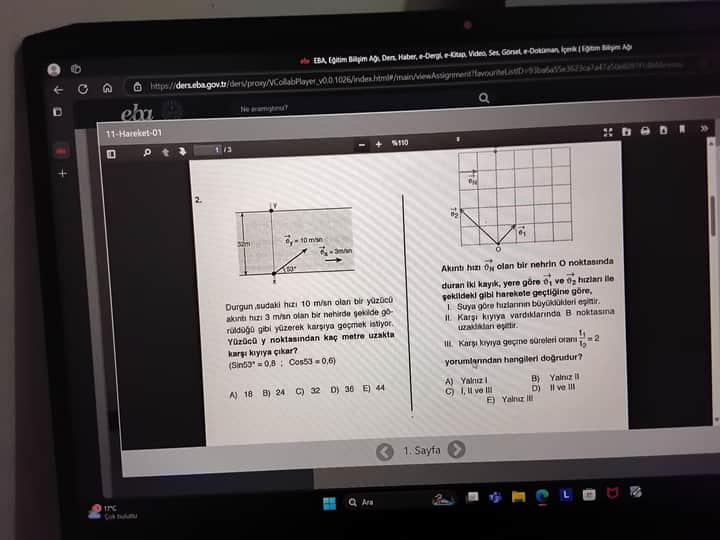
Yüzücü sorusunun çözümü:

Yüzücünün suya göre hızı v_{y} = 10 \, \text{m/s} ve akıntı hızı v_{a} = 3 \, \text{m/s}'dir. Yüzücü, 53^\circ açıyla akıntıya karşı yüzmekte. Yüzücünün suya göre hızı bileşenlerine ayırabiliriz:

  • Y ekseni boyunca (dik) hız: v_{y} \cdot \sin(53^\circ) = 10 \cdot 0.8 = 8 \, \text{m/s}
  • X ekseni boyunca (akıntıya paralel) net hız: v_{y} \cdot \cos(53^\circ) - v_{a} = 10 \cdot 0.6 - 3 = 6 - 3 = 3 \, \text{m/s}

Y yüzeyinden geçmek için gereken süreyi bulmak için 32 m’lik dikey mesafeyi alırız:

t = \frac{\text{mesafe}}{\text{dik hız}} = \frac{32}{8} = 4 \, \text{s}

Bu süre içerisinde yüzücünün akıntıya göre ne kadar sürükleneceğini bulmak için yanal hareket hesaplanır:

x = \text{net yanal hız} \times t = 3 \times 4 = 12 \, \text{m}

Yani, yüzücü Y noktasından 12 metre uzakta kıyıya çıkar. Ancak seçenekler arasında 12 m yok. Olası seçenek hatalarına karşın, akıntıya paralel hız bileşeni dikkate alındığında sonuç bu şekildedir.

5

Cevap nedir anlamadim

6

Elbette, daha detaylı açıklayayım.

Sorunun Çözümü:

  1. Verilen Değerler:

    • Yüzücünün suya göre hızı: 10 m/s
    • Nehrin akıntı hızı: 3 m/s
    • Yüzücünün yüzerken yaptığı açı: 53°
    • Dikey mesafe (nehir genişliği): 32 m

  2. Yüzücünün Dikey ve Yatay Hız Bileşenleri:

    • Dikey hız bileşeni (karşı kıyıya doğru):
      v_{\text{dikey}} = 10 \cdot \sin(53°) = 10 \cdot 0.8 = 8 \, \text{m/s}
    • Yatay hız bileşeni (akıntı yönünde):
      v_{\text{yanal}} = 10 \cdot \cos(53°) - 3 = 6 - 3 = 3 \, \text{m/s}

  3. Zaman Hesabı:

    • Karşı kıyıya ulaşmak için gereken zaman:
      t = \frac{32}{8} = 4 \, \text{s}

  4. Yanlamasına Sürüklenme Mesafesi:

    • Bu zaman zarfında yatayda alınan mesafe:
      x = v_{\text{yanal}} \times t = 3 \times 4 = 12 \, \text{m}

Sonuç:

Yüzücü, başlangıç noktasından 12 metre yan tarafa sürüklenerek karşı kıyıya ulaşır. Ancak seçenekler arasında doğru değer yok. Bu matematiksel hesaplamalara göre sonuç 12 metredir.

7

20241013_215609
20241013_215609720×540 31.9 KB

8

Görseldeki soruyu yazıyla belirtirsen, çözüm için yardımcı olabilirim.