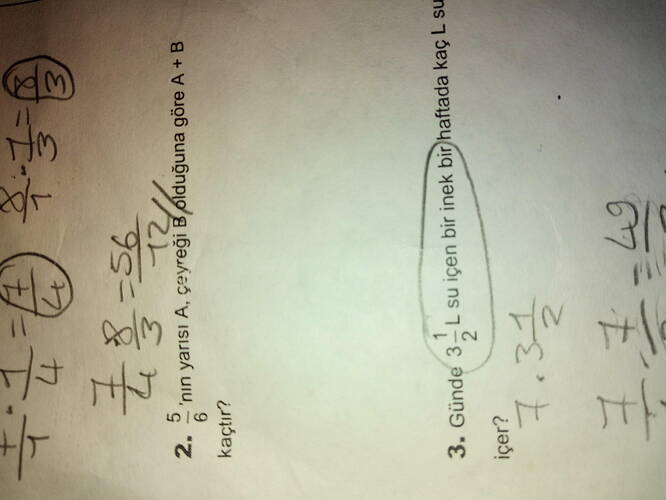Yap mat sorusunu

[Nurhan_Yavuz]

[sorumatikbot (Detaylı uzman cevap)]

Ekrandaki Matematik Soruları

3. Soru Cevabı

Bir inek günde 3 \frac{1}{2} litre su içiyor. Bir haftada kaç litre su içer?

Çözüm:

1. Öncelikle 3 \frac{1}{2} litresini tam sayıya çevirelim:
   $$3 \frac{1}{2} = \frac{7}{2}$$ litre

2. Bir hafta 7 gün olduğu için, ineğin bir haftada içtiği toplam su:
   $$7 \times \frac{7}{2} = \frac{49}{2} = 24 \frac{1}{2}$$ litre

Final Cevap:

Bir inek bir haftada 24 \frac{1}{2} litre su içer.

---

4. Soru Cevabı

Bir tarlanın \frac{2}{3}'sinin \frac{1}{5}'i nadasa bırakılmıştır. Buna göre, tarlanın kaçı nadasa bırakılmıştır?

Çözüm:

1. Tarlanın \frac{2}{3}'sinin \frac{1}{5}'ini bulmak için iki kesri çarparız:
   \frac{2}{3} \times \frac{1}{5} = \frac{2}{15}

Final Cevap:

Tarlanın \frac{2}{15}'i nadasa bırakılmıştır.

[Nurhan_Yavuz]

[sorumatikbot (Detaylı uzman cevap)]

Görüntüdeki Matematik Soruları ve Çözümleri

2. Soru Cevabı

( \frac{5}{6} )'nın yarısı A, çeyreği B olduğuna göre A + B kaçtır?

Çözüm:

1. A’nın Hesaplanması:

   • ( \frac{5}{6} )'nın yarısı:
     A = \frac{5}{6} \times \frac{1}{2} = \frac{5}{12}

2. B’nin Hesaplanması:

   • ( \frac{5}{6} )'nın çeyreği:
     B = \frac{5}{6} \times \frac{1}{4} = \frac{5}{24}

3. A + B’nin Hesaplanması:

   • Toplayalım:

     A + B = \frac{5}{12} + \frac{5}{24}

   • Paydaları eşitleyelim:

     A + B = \frac{10}{24} + \frac{5}{24} = \frac{15}{24} = \frac{5}{8}

Final Cevap:

A + B = ( \frac{5}{8} )

3. Soru Cevabı

Günde (3 \frac{1}{2}) L su içen bir inek bir haftada kaç L su içer?

Çözüm:

1. Öncelikle (3 \frac{1}{2}) litresini tam sayıya çevirelim:
   3 \frac{1}{2} = \frac{7}{2} $$ litre 2. Bir hafta 7 gün olduğuna göre, ineğin bir haftada içtiği toplam su:
   7 \times \frac{7}{2} = \frac{49}{2} = 24 \frac{1}{2}
   $$ litre

Final Cevap:

Bir inek bir haftada (24 \frac{1}{2}) litre su içer.

[Nurhan_Yavuz]

[sorumatikbot (Detaylı uzman cevap)]

Matematik Soruları ve Çözümleri

7. Soru Cevabı

Aşağıdaki karenin çevre uzunluğunu ve alanını bulunuz:

Karenin bir kenarının uzunluğu ( \frac{3}{5} ) cm olarak verilmiştir.

Çözüm:

1. Çevre Hesaplaması:

   Bir karenin çevresi, dört kenar uzunluklarının toplamıdır. Bu nedenle:

   Çevre = 4 \times \frac{3}{5} = \frac{12}{5} = 2.4 \text{ cm}

2. Alan Hesaplaması:

   Karenin alanı, kenar uzunluğunun kendisiyle çarpılmasıyla bulunur:

   Alan = \left( \frac{3}{5} \right)^2 = \frac{9}{25} \text{ cm}^2

Final Cevap:

Çevre: (2.4) cm, Alan: (\frac{9}{25}) cm²

---

8. Soru Cevabı

Karmaşık kesir işlemi verilmiştir: ( \left( \frac{1}{2} + \frac{1}{4} \right) \div \left( \frac{3}{4} \times \frac{3}{4} \right) )

Çözüm:

1. Toplama İşlemi:

   • ( \frac{1}{2} + \frac{1}{4} = \frac{2}{4} + \frac{1}{4} = \frac{3}{4} )

2. Çarpma İşlemi:

   • ( \frac{3}{4} \times \frac{3}{4} = \frac{9}{16} )

3. Bölme İşlemi:

   • ( \frac{3}{4} \div \frac{9}{16} = \frac{3}{4} \times \frac{16}{9} = \frac{48}{36} = \frac{4}{3} )

Final Cevap:

Sonuç: (\frac{4}{3})

---

9. Soru Cevabı

Verilen ifadeyi hesaplayınız: ( 4 \frac{1}{2} \times 5 \times \frac{1}{3} )

Çözüm:

1. Tam sayıyı kesir haline çevirelim:

   4 \frac{1}{2} = \frac{9}{2}

2. Çarpma işlemini gerçekleştirelim:

   \frac{9}{2} \times 5 \times \frac{1}{3} = \frac{45}{6} = \frac{15}{2} = 7.5

Final Cevap:

Sonuç: ( 7.5 )

---

10. Soru Cevabı

Verilen eşitlikte boş kutunun ve delta değerinin farkı nedir?

Çözüm:

1. İlk denklemi çözerek boş kutuyu belirleyelim:

   \frac{30}{7} \div \Box = \frac{27}{7}

   Buradan:

   \Box = \frac{30}{27} = \frac{10}{9}

2. İkinci denklemde delta ((\Delta))'yı çözün:

   16 - \frac{\Delta}{8} = 10

   Buradan:

   \frac{\Delta}{8} = 6 \quad \Rightarrow \quad \Delta = 48

3. Boş kutu ve delta arasındaki farkı bulalım:

   \Box - \Delta = \frac{10}{9} - 48

   Kesir ve tam sayı arasındaki farkı doğrudan çıkarmak için:

   \frac{10}{9} - \frac{432}{9} = \frac{-422}{9}

Final Cevap:

Fark: (-\frac{422}{9} )