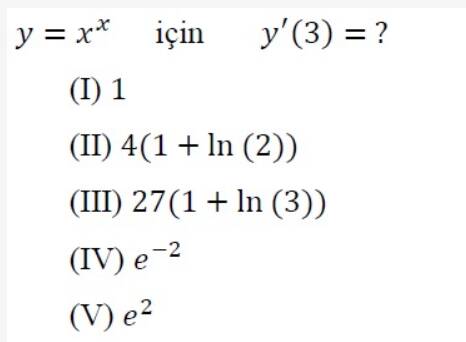( y = x^x ) için ( y’(3) = ? )
Cevap:
Bu tür bir fonksiyonun türevini bulmak için, önce doğal logaritma alarak fonksiyonu daha yönetilebilir bir hale getirebiliriz. Şu adımları izleyelim:
- Fonksiyonu Daha Kolay Bir Hale Getirin:
( y = x^x )
\ln(y) = \ln(x^x) = x \ln(x)
- Her iki tarafın türevini alın:
\frac{d}{dx}(\ln(y)) = \frac{d}{dx}(x \ln(x))
- Türevleri hesaplayın:
\frac{1}{y} \cdot y' = \ln(x) + 1
- Türevini bulmak istediğimizi izole edin:
y' = y (\ln(x) + 1)
Burada ( y = x^x ) olduğuna göre, yerine koyarsak:
y' = x^x (\ln(x) + 1)
- Verilen noktada (x=3) türevi hesaplayın:
y'(3) = 3^3 (\ln(3) + 1) = 27 (\ln(3) + 1)
Bu hesaplamaların sonucuna göre, doğru seçenek:
\boxed{27(1 + \ln(3))} seçeneğidir, yani (III).