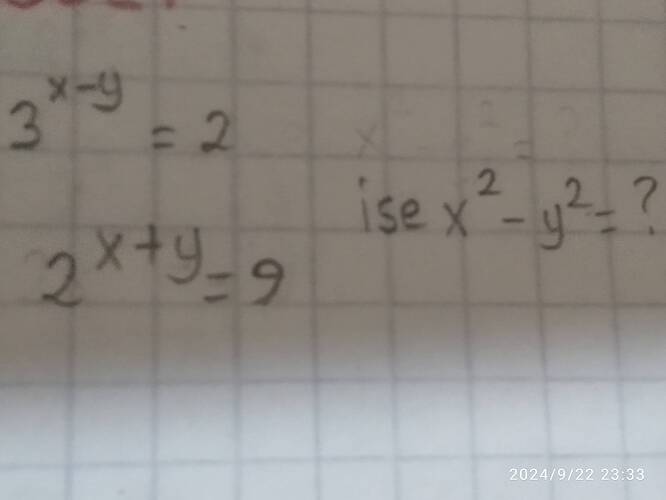Verilen denklemler doğrultusunda ( x^2 - y^2 ) nedir?
Çözüm:
Verilen denklemler:
- ( 3^{x-y} = 2 )
- ( 2^{x+y} = 9 )
Bu denklemleri kullanarak ( x^2 - y^2 ) ifadesini bulacağız. İlk olarak denklemleri logaritma veya üstel fonksiyon kullanarak çözebiliriz.
Adım 1: ( x-y ) ve ( x+y ) için ifade bulma
İlk Denklem:
3^{x-y} = 2
Her iki tarafın logaritmasını alarak:
(x-y) \cdot \log 3 = \log 2
Buradan:
x-y = \frac{\log 2}{\log 3}
İkinci Denklem:
2^{x+y} = 9
Her iki tarafın logaritmasını alarak:
(x+y) \cdot \log 2 = \log 9
Buradan:
x+y = \frac{\log 9}{\log 2}
Adım 2: ( x^2 - y^2 ) İfadesini Bulma
( x^2 - y^2 ) ifadesi, ((x-y)) ve ((x+y)) çarpımı olarak açılabilir:
x^2 - y^2 = (x-y)(x+y)
Bulduğumuz ifadeleri yerine koyalım:
x^2 - y^2 = \left(\frac{\log 2}{\log 3}\right)\left(\frac{\log 9}{\log 2}\right)
Burada, (\log 2) terimleri birbirini götürür:
x^2 - y^2 = \frac{\log 9}{\log 3}
Sonuç:
( \log 9 = 2 \log 3 ) olduğundan:
x^2 - y^2 = \frac{2 \log 3}{\log 3} = 2
Bu durumda, cevap ( \boxed{2} ) olur.