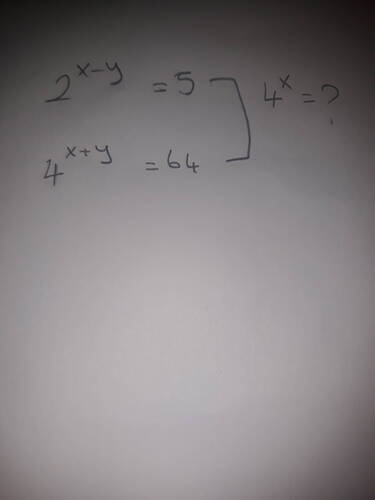Verilen denklemleri çözerek 4^x değerini bulalım.
Denklemlerimiz şunlar:
- 2^{x-y} = 5
- 4^{x+y} = 64
İkinci denklemi sadeleştirerek başlayalım:
$$ 4^{x+y} = 64 $$
64, 4^3 olarak yazılabilir. Bu durumda denklemi şöyle yazabiliriz:
$$ 4^{x+y} = 4^3 $$
Tabanlar aynı olduğu için, üsleri eşitleyebiliriz:
$$ x + y = 3 ,,, (3) $$
Şimdi, 2^{x-y} = 5 denklemine geri dönelim. Bu denklemi de başka bir şekilde yazabiliriz:
$$ (2^2)^{x-y} = 5^2 $$
Bu nedenle:
$$ 4^{x-y} = 25 $$
Üçüncü denklemi ve biraz önce bulduğumuz x+y = 3 denklemini kullanarak x ve y'yi bulalım.
Adım 1: x ve y'yi Bulmak
x-y = \log_4 25
x+y = 3
Bu iki denklemi toplayarak 2x'i bulmak istiyoruz:
$$(x-y) + (x+y) = \log_4 25 + 3$$
$$2x = \log_4 25 + 3$$
x = \frac{\log_4 25 + 3}{2}
Şimdi 4^x'i ifade edelim:
$$4^x = 4^{\frac{\log_4 25 + 3}{2}}$$
Bu çözümle daha fazla ilerlemek için \log_4 25'in yaklaşık değerini kullanmak gerekir, fakat burada işlemin özünü belirledik: 4^x değeri x'in bu formülü ile hesaplanabilir.
Özet: İki verilen denklem kullanılarak x'i ve oradan da 4^x'i bulabilirsiniz. Ancak detaylı hesaplamalar için logaritma değerini bilmek veya bir hesap makinesi kullanmak gerekebilir.