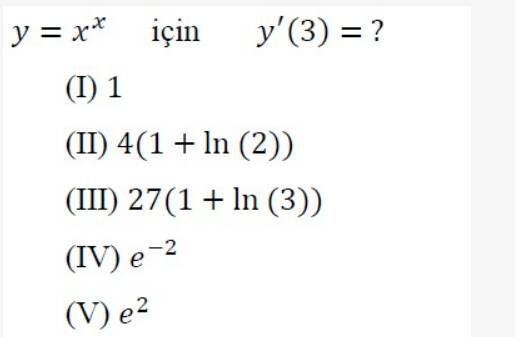Y = x^x için y’(3) =?

Üniversite Matematik Bölümü
1

aaaaaaaa
aaaaaaaa515×337 11.3 KB

2

y = x^x için y’(3) = ?

Cevap:
Bu soruyu çözmek için y = x^x fonksiyonunun türevini hesaplamamız gerekmektedir.

  1. Fonksiyonun Doğal Logaritmasını Almak:

    • Öncelikle y = x^x fonksiyonunun doğal logaritmasını alalım:
      \ln y = \ln(x^x)
    • Logaritmanın özelliklerini kullanarak açalım:
      \ln y = x \ln x

  2. Her İki Tarafın Türevini Almak:

    • Her iki tarafın türevini alalım (zincir kuralını kullanarak):
      \frac{d}{dx} (\ln y) = \frac{d}{dx} (x \ln x)
    • Sol tarafın türevi:
      \frac{1}{y} \frac{dy}{dx}
    • Sağ tarafın türevi (ürün kuralı):
      \ln x + x \cdot \frac{1}{x} = \ln x + 1

  3. Elde Ettiğimiz Türevleri Birleştirmek:

    • Elde ettiğimiz türev ifadelerini birleştirelim:
      \frac{1}{y} \frac{dy}{dx} = \ln x + 1
    • Şimdi dy/dx’i yalnız bırakıyoruz:
      \frac{dy}{dx} = y (\ln x + 1)
    • y = x^x olduğuna göre yerine koyarsak:
      \frac{dy}{dx} = x^x (\ln x + 1)

  4. y' (3) Hesaplamak:

    • x = 3 için türevi hesaplayalım:
      y' (3) = 3^3 (\ln 3 + 1)
    • 3^3 = 27 olduğuna göre yerine koyarsak:
      y' (3) = 27 (1 + \ln 3)

Bu durumda cevap (III) seçeneğidir:

\boxed{27(1 + \ln(3))}