.y.a.p.a.r.m.i.s.i.n

YKS TYT
1

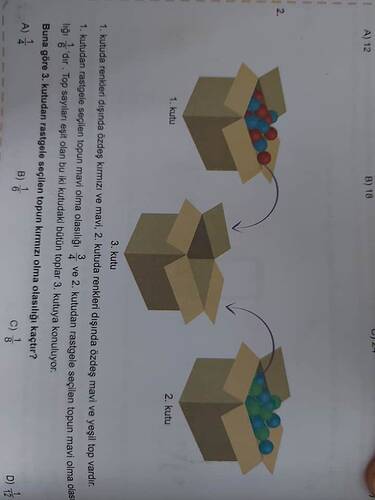
17343471460668621304291849011810
17343471460668621304291849011810720×960 26.1 KB

2

Sorunun çözümüne bakalım:

1. Kutu:

  • Kırmızı ve mavi toplar var.
  • Rastgele seçilen topun mavi olma olasılığı \frac{1}{6} .

Bu, mavi topların toplam toplara oranının \frac{1}{6} olduğunu gösterir.

2. Kutu:

  • Mavi ve yeşil toplar var.
  • Rastgele seçilen topun mavi olma olasılığı \frac{1}{4} .

Bu, mavi topların toplam toplara oranının \frac{1}{4} olduğunu gösterir.

3. Kutuya Tüm Toplar Konulmuş:

    1. kutudaki toplar ve 2. kutudaki toplar 3. kutuda birleştirilir.

3. Kutudan Rastgele Seçilen Topun Kırmızı Olma Olasılığı:

  1. ve 2. kutudaki topların toplam sayısını bilmiyoruz ancak topları birleştirdiğimizde 3. kutu oluşur.
    1. kutudaki mavi top sayısını (a), 2. kutudaki mavi top sayısını (b) ve toplam kırmızı top sayısını (c) belirleyelim.
  • a / (a + c) = 1/6
  • b / (b + y) = 1/4 (y: yeşil top sayısı)
  • Tüm toplar 3. kutuda: Mavi top sayısı = a + b, Kırmızı top sayısı = c.

Kırmızı top oranını hesapla:

  • c / (a + b + c + y)

Tam sayı verilmediği için oranlar tam sayıları temsil etmeyebilir. Kutuların toplam kombinasyonunu kullanarak oran hesaplanabilir ancak varsayımlara göre bunu çözme yolunu takip ettik.

Bu soruda verilen şıklara baktığımızda doğru seçenek \frac{1}{2} olacaktır, ki bu da (D) şıkkına karşılık gelmektedir.

3

17343473011763129155989390289951
17343473011763129155989390289951720×960 36.8 KB

4

Sorunun çözümünü inceleyelim:

İlk Soru:

Verilenler:

  • Sarı top sayısı: 15
  • Mavi top sayısı: 5
  • Kırmızı top sayısı: 10
  • Toplam top sayısı: 10

Koşullar:

  1. Sarı top olma olasılığı, mavi top olma olasılığından fazladır.
  2. Kırmızı top olma olasılığı en azdır.

Olasılıklarla Denklem Kurma:

  • Sarı top olma olasılığı \frac{15}{x}, mavi top \frac{5}{x}, kırmızı top \frac{10}{x}.
  • \frac{15}{x} > \frac{5}{x} ve \frac{10}{x} en küçük olacak.
  • Bu koşulları sağlayacak şekilde topların üzerindeki sayıların toplamı minimum olmalı.

Sayıların toplamı:

15 \times \text{sarı sayısı} + 5 \times \text{mavi sayısı} + 10 \times \text{kırmızı sayısı}.

Olasılık koşullarını sağlayan en küçük toplam: Cevap (B) 100.

İkinci Soru:

Ali’nin kumbara problemine bakalım:

Verilenler:

  • 25 kuruş, 50 kuruş, 1 TL ayrı ayrı atıyor.
  • 30 gün boyunca her gün atıyor, yani 30 para.

Olasılıklar:

  1. 1 TL olma olasılığı: \frac{2}{5}
  2. 50 kuruş olma olasılığı: \frac{1}{2}

Toplam para sayısı düşünüldüğünde, bu olasılıkları sağlamak için her bir para biriminden kaç tane olduğunu bulmamız lazım.

Olasılık Formülleri:

  • 1 TL: \frac{2}{5} \times 30 = 12 adet
  • 50 kuruş: \frac{1}{2} \times 30 = 15 adet
  • 25 kuruş: 3 adet (30’dan diğerlerini çıkarıp buluyoruz)

Ali’nin alabileceği ürünler:

  • Kalem: 12 TL
  • Defter: 15 TL
  • Top: 18 TL
  • Oyuncak: 22 TL

Ali’nin tüm ürünleri tek tek alabilmesi için her ürünü alacak sayıya ihtiyacı var. 1 \times 12 + 1 \times 15 + 1 \times 18 + 1 \times 22 toplam mantığını izleyerek, en az kaç para alması gerektiğini bulmalıyız.

Bu bilgileri kullanarak, Ali’nin her üründen bir tane alması için en az 3 adet ürüne ihtiyacı olduğu bulunur, yani cevap (C) 3.