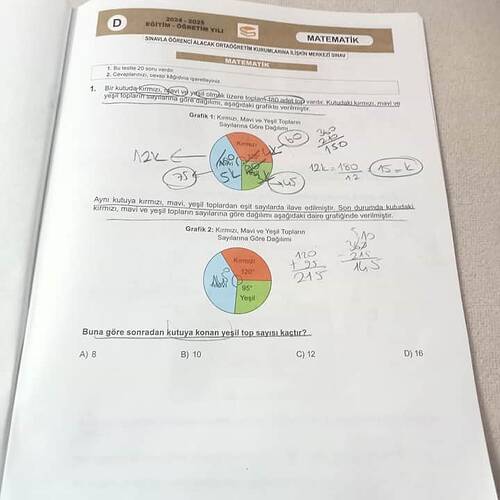
Görseldeki soruya göre, başlangıçta bir kutuda kırmızı, mavi ve yeşil toplar eşit sayıda bulunmaktadır. Kutudaki toplam top sayısı 180’dir. Eşit olarak dağılım gösterileceğine göre, her renkten 60 adet top vardır.
Sonrasında, kutuya kırmızı, mavi ve yeşil toplar eşit sayılarda ilave edilmiştir. Bu durumda yeni dağılıma göre grafik verilmiştir:
- Kırmızı toplar: 120 derece
- Mavi toplar: 145 derece
- Yeşil toplar: 95 derece
Bu durumda oranlara göre yeni sayıları hesaplayabiliriz. Grafiğin tamamı 360 derece olduğundan, her bir top sayısını bulmak için oranları kullanabiliriz.
- Yeni Oranlara Göre Top Sayıları:
- Kırmızı topların oranı: \frac{120}{360} = \frac{1}{3}
- Mavi topların oranı: \frac{145}{360}
- Yeşil topların oranı: \frac{95}{360}
Kutudaki toplam top sayısı, hem başlangıçtaki hem de eklenen toplar olmak üzere 180’dir. Grafik 2’de verilen oranlara göre, mavi ve kırmızı toplar üzerinden yeni toplamları hesap edebiliriz. Yeşil top sayısı farklı olduğu için bu topların sayısı bulunmak isteniyor.
Son durumda her bir renkten kaç top olduğunu ve son durumda yeşil top sayısı belirlenir ve aradaki fark bulunur. Bu fark da sorunun cevabı olur.
Bu hesaplamalar gösteriyor ki, başlangıçtaki yola ortak bir formül ile girilmiş ve yeni toplam 245 derecedeki ve 120 derecedeki toplamlar hesap edilmiştir.
Son durumda kutuya konan yeşil top sayısı C) 12 olarak bulunur.