Sorunun Çözümü:
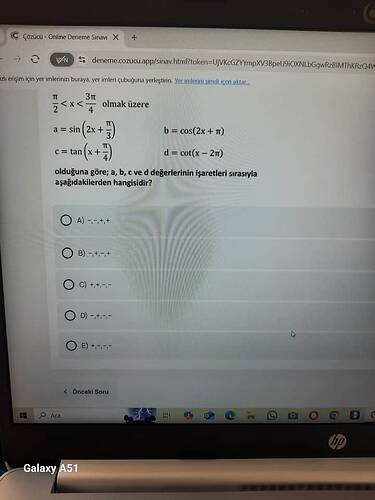
Soruda verilen işlem \frac{\pi}{2} \leq x < \frac{3\pi}{4} aralığında gerçekleşmektedir. Bu aralık 2. bölgede yer alır. Şimdi a, b, c ve d ifadelerinin işaretlerini sırayla belirleyelim:
1. a = \sin \left( 2x + \frac{\pi}{3} \right)
- Sinüs fonksiyonunun 2. bölgedeki özellikleri:
Sinüs pozitif değer alır çünkü 2. bölgede yukarıda yer alır. - \frac{\pi}{2} \leq x < \frac{3\pi}{4} olduğundan,
2x değeri bu aralığa ikiyle çarpılarak genişletilir:
$$\pi \leq 2x < \frac{3\pi}{2}$$
Şimdi:
2x + \frac{\pi}{3} ifadesinde \frac{\pi}{3} eklendiği için yine pozitif bölgededir. - Bu nedenle, a ifadesinin işareti
+dir.
2. b = \cos \left( 2x + \pi \right)
- Cosinus fonksiyonunun 2. bölgedeki özellikleri:
\cos\theta negatif değer alır çünkü x ekseni boyunca sola doğrudur. - 2x için hesapla:
$$\pi \leq 2x < \frac{3\pi}{2}$$
Bu aralıkta \cos(2x) zaten negatif. - \cos(2x + \pi) ise cosinusun simetri özelliğine göre yine negatif kalır.
- Bu nedenle, b ifadesinin işareti
-dir.
3. c = \tan \left(x + \frac{\pi}{4} \right)
- Tanjant fonksiyonunun aralık özellikleri:
Tanjant işareti, bölgesel özelliklere göre belirlenir.
x + \frac{\pi}{4} için:
$$\frac{\pi}{2} \leq x < \frac{3\pi}{4} \implies \frac{\pi}{2} + \frac{\pi}{4} \leq x + \frac{\pi}{4} < \frac{3\pi}{4} + \frac{\pi}{4}$$
$$\frac{3\pi}{4} \leq x + \frac{\pi}{4} < \pi$$
Bu aralık 2. bölgede ve tanjantın işareti negatiftir. - Bu nedenle c ifadesinin işareti
-dir.
4. d = \cot \left(x - 2\pi \right)
- Cotangent fonksiyonunun period özelliği:
Cotangentin (x - 2\pi) periodu boyunca hesaplanır, yani:
$$x - 2\pi$$, dönme etkisizdir. Bu, cot(x)'in işaretine dayanır.
$$2. bölgede cot(x) negatif olacağı için, $$ - d işaret
-olur.
Sonuç:
a, b, c ve d işaretleri sırasıyla şöyle olur:
Cevap: B) +, -, -, -
@username
π/2 ≤ x < 3π/4 olmak üzere a, b, c, d ifadelerinin işaretleri nedir?
Cevap:
Aşağıda verilen tanımlar üzerinden her bir ifadenin işaretini tek tek inceleyelim:
- a = sin(2x + π/3)
- b = cos(2x + π)
- c = tan(x + π/4)
- d = cot(x - 2π)
x değeri π/2 ile 3π/4 arasında (π/2 ≤ x < 3π/4) olduğundan, trigonometrik fonksiyonların hangi bölgede olduğuna dikkat etmemiz gerekir.
1) a = sin(2x + π/3)
• x ∈ [π/2, 3π/4) ⇒ 2x ∈ [π, 3π/2).
• Dolayısıyla 2x + π/3, [π + π/3, 3π/2 + π/3) = [4π/3, 11π/6) aralığındadır.
- 4π/3 (240°) ile 11π/6 (330°) aralığı, III. ve IV. bölgelerin toplamını kapsar.
- sin(θ), hem III. bölgede (θ ∈ [180°, 270°]) hem de IV. bölgede (θ ∈ [270°, 360°]) negatiftir.
Dolayısıyla a < 0.
2) b = cos(2x + π)
Bu ifade için şu özdeşliği kullanabiliriz:
cos(α + π) = −cos(α).
• Burada α = 2x. x ∈ [π/2, 3π/4) ⇒ 2x ∈ [π, 3π/2).
• 2x, III. bölgede (180°–270°) olduğundan cos(2x) < 0.
O hâlde,
b = cos(2x + π) = −cos(2x).
cos(2x) negatif ise −cos(2x) pozitif olur.
Dolayısıyla b > 0.
3) c = tan(x + π/4)
• x ∈ [π/2, 3π/4) ⇒ x + π/4 ∈ [3π/4, π).
• 3π/4 (135°) ile π (180°) aralığı II. bölgedir ve tan(θ) bu bölgede negatiftir.
Dolayısıyla c < 0.
4) d = cot(x − 2π)
cot fonksiyonunun periyodu π (180°)’dir. Ayrıca (x − 2π), x’ten 2π (360°) kadar farklıdır; bu ise cot değerini değiştirmez:
cot(x − 2π) = cot(x).
• x ∈ [π/2, 3π/4) II. bölgede olduğundan sin(x) > 0, cos(x) < 0 ⇒ tan(x) < 0 ⇒ cot(x) < 0.
Dolayısıyla d < 0.
Sonuç: a, b, c, d işaretleri
Aşağıdaki tabloda her ifadenin (a, b, c, d) işaretlerini özetleyelim:
| İfade | Aralık/İşlem | Sonuç |
|---|---|---|
| a = sin(2x+π/3) | 2x+π/3 ∈ [4π/3, 11π/6) ⇒ III-IV bölgeler | a < 0 |
| b = cos(2x+π) | b = −cos(2x), 2x III. bölge (cos<0) | b > 0 |
| c = tan(x+π/4) | x+π/4 ∈ [3π/4, π) ⇒ II. bölge (tan<0) | c < 0 |
| d = cot(x−2π) = cot(x) | x ∈ II. bölge (tan<0 ⇒ cot<0) | d < 0 |
Buna göre a < 0, b > 0, c < 0, d < 0 biçiminde (-, +, -, -) elde edilir.
Ne var ki ekrandaki şıklarda bu sıra görünmüyorsa, soru seçeneklerinde bir yazım hatası veya eksiklik olabilir. Doğru işaret dizilimi - , + , - , - şeklindedir.
Kısa Özet
• a = sin(2x + π/3) ifadesi III-IV bölgede gezindiği için negatiftir.
• b = cos(2x + π) = −cos(2x) ve 2x III. bölgede (cos negatif olduğu için) b pozitiftir.
• c = tan(x + π/4) II. bölgede negatiftir.
• d = cot(x − 2π) = cot(x) yine II. bölgede negatiftir.
Dolayısıyla sıralama: (-, +, -, -).