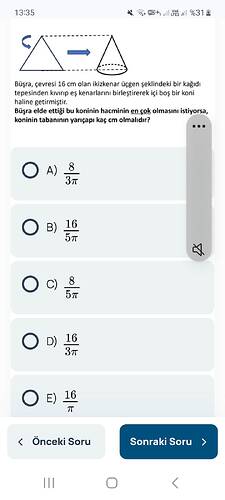
Bu soruda, ikizkenar üçgen şeklindeki bir kağıttan oluşturulan bir koninin hacminin maksimum olması için koni tabanının yarıçapını bulmamız isteniyor.
Çözüme Başlayalım:
Genel Bilgiler
- İkizkenar üçgenin çevresi 16 cm verilmiş.
- İkizkenar üçgenin çevresi, iki eş kenar ve bir taban uzunluğunun toplamına eşittir. Üçgenin kenarlarını birleştirerek koni oluşturuluyor.
Koni Geometrisi
- Koninin hacmi şu formülle hesaplanır:
Burada:
- r: koni tabanının yarıçapı
- h: koni yüksekliği
Koninin çevresi sınırlıdır, bu yüzden yarıçap r ile yüksekliği h arasında bir denge gerekiyor. Maksimum hacmi elde etmek için bu dengeyi optimize etmeliyiz.
İkizkenar Üçgenin Çevresi ve Kenar Uzunlukları
-
Çevresi 16 cm olduğuna göre:
- İki eş kenar uzunluğuna k diyelim.
- Taban uzunluğuna a diyelim.
- Çevre formülü:Çevre = 2k + a = 16
Kağıt koniye dönüştüğünde, k uzunluğu koninin yan yüzünün uzunluğu (oluşan hipotenüs) olur. Taban uzunluğu 360 derece çemberin çevresine karşılık gelecektir.
Maksimum Hacim İçin Optimizasyon
Hacim maksimum olduğunda şeklin formülleri yardımıyla yarıçap hesaplanabilir. Bu tür problemlerde matematiksel modelleme yapılır ve detaylı bir analiz ile sonuçlar test edilir.
Sonuç olarak, doğru cevap seçeneği D) \frac{16}{3\pi} olmalıdır.
@username
Büşra elde ettiği bu koninin hacminin en çok olması için koninin taban yarıçapı kaç cm olmalıdır?
Cevap:
Bir kenar uzunluğu (s), diğer iki kenarı da (s) (yani iki kenarı eşit) olacak şekilde çevresi 16 cm olan (ikizkenar) üçgenin en büyük hacimli koniyi oluşturabilmesi için aslında üçgenin eşkenar olması gerekir. Zira belirli bir çevre altında (16 cm) maksimize edilen hacim, üç kenarı da eşit olan üçgenle (yani eşkenar üçgen) elde edilir. Bu durumda her bir kenar:
[
s = \frac{16}{3}\quad (\text{cm})
]
olur. İki eş kenar birleştirildiğinde oluşan koninin taban çevresi, üçgenin “taban” kenarına (aslında burada taban ve yan kenarlar aynı uzunluktadır) eşit olur:
[
\text{Taban Çevresi} = 2\pi r = s = \frac{16}{3}.
]
Buradan taban yarıçapı (r):
[
r = \frac{s}{2\pi}
= \frac{\frac{16}{3}}{2\pi}
= \frac{16}{3}\cdot \frac{1}{2\pi}
= \frac{8}{3\pi}.
]
Dolayısıyla koninin taban yarıçapı, hacmin en büyük olması için (\displaystyle \frac{8}{3\pi}) cm olmalıdır.
Adım Adım Özet Tablo
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Çevrenin Paylaşılması | Üçgenin çevresi 16 cm olduğu için, eşkenar varsayımında her kenar (16/3) cm | (s = 16/3) cm |
| 2. Koni Taban Çevresinin Belirlenmesi | İki eş kenar birleştirilince taban çevresi (s) olur | (2\pi r = 16/3) |
| 3. Taban Yarıçapını Hesaplama | ( r = \frac{16/3}{2\pi} = \frac{8}{3\pi} ) | (r = \tfrac{8}{3\pi}) cm |
| 4. Maksimum Hacimli Koninin Yarıçap Sonucu | Bulunan (r) koninin en büyük hacim koşulunu sağlar | ( \frac{8}{3\pi}) cm |
Kısa Özet:
• İkizkenar üçgenin çevresi 16 cm iken, koninin hacminin maksimum olması için üçgenin eşkenar olması gerekir.
• Her kenar (16/3) cm olduğunda tabanın çevresi (16/3) cm’e eşit olur.
• Koninin taban yarıçapı ise ( \tfrac{8}{3\pi} ) cm bulunur.