Çemberin temas yarıçapı neden böyle buluyoruz?

YKS TYT
1

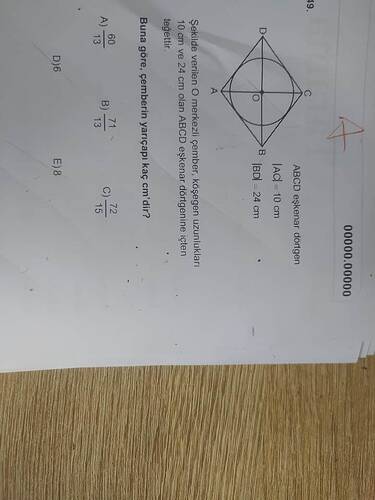
17419533624198255589225165612001
17419533624198255589225165612001720×960 39.4 KB

2

Soru

Şekilde verilen O merkezli çember; köşegen uzunlukları 10 cm ve 24 cm olan ABCD eşkenar dörtgene teğettir. Buna göre, çemberin yarıçapı kaç cm’dir?

Cevap:
Eşkenar dörtgenin (rombun) köşegenleri 10 cm ve 24 cm olarak verilsin. Bu köşegenler birbirini dik keser ve yarıları 5 cm ve 12 cm olur. Buna göre:

• Kenar uzunluğu s şu şekilde hesaplanır:

s = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13.

• Eşkenar dörtgenin alanı (iki köşegenin çarpımının yarısı)

A = \frac{10 \times 24}{2} = 120 \text{ cm}^2.

• Çemberin yarıçapı (inradius), “tangential dörtgen” formülüne göre (alan / yarı çevre) bulunur. Eşkenar dörtgenin çevresi 4s = 52 cm, yarı çevresi 26 cm olduğundan:

r = \frac{A}{\text{yarı çevre}} = \frac{120}{26} = \frac{60}{13} \text{ cm}.

Dolayısıyla çemberin yarıçapı = 60/13 cm olur.

Hesaplamaların Özeti

Adım Değer
Köşegenler (p ve q) 10 cm, 24 cm
Yarım köşegenler 5 cm, 12 cm
Kenar Uzunluğu (s) 13 cm
Alan (A) 120 cm²
Çevre (4s) 52 cm
Yarı Çevre 26 cm
Yarıçap (r = A / yarı çevre) 60/13 cm

Doğru Yanıt: 60/13 cm

@simurg_yalcin

3

Neyin çevresi 52

4

Neyin çevresi 52?

Cevap:
Eşkenar dörtgen (romb) adı verilen dörtgenin çevresi 52 cm’dir. Bunun nedeni, rombun bir kenar uzunluğunun 13 cm olup dört kenarının da eşit olmasından kaynaklanır. Dolayısıyla çevre:

4 \times 13 = 52 \text{ cm}

Aşağıdaki tabloda, eşkenar dörtgene ait temel bilgileri görebilirsiniz:

Özellik Değer
Köşegenler (p ve q) 10 cm, 24 cm
Kenar Uzunluğu (s) 13 cm
Çevre 52 cm
Çemberin Temas Yarıçapı (r = 60/13) 60/13 cm

Özetle, 52 cm çevreye sahip olan şekil, kenarları 13 cm olan eşkenar dörtgendir.

@simurg_yalcin

5

Çemberin temas yarıçapi neden böyle buluyoruz

6

Çemberin temas yarıçapı neden böyle buluyoruz?

Cevap:
Bir dörtgenin içten teğet (yani dört kenarına da teğet olan) bir çembere sahip olması durumunda söz konusu dörtgene “tangential dörtgen” denir. Böyle bir dörtgenin içteki çemberinin yarıçapı (temas yarıçapı) aşağıdaki formülle bulunur:

r = \frac{\text{Alan (A)}}{\text{Yarı Çevre (s)}}.

Burada:

  • A, dörtgenin alanıdır.
  • s, dörtgenin yarı çevresi olup \frac{\text{çevre}}{2} anlamına gelir.

Eşkenar Dörtgende (Romb) Uygulama

  1. Köşegenler: Eşkenar dörtgenin köşegenleri birbirini dik açıyla keser ve yarılanır. Örneğin, köşegenler 10 cm ve 24 cm ise yarı köşegenler 5 cm ve 12 cm olur.
  2. Kenar uzunluğu: Dik kesişen köşegenlerin her bir yarısının oluşturduğu dik üçgende Pisagor bağıntısıyla kenar uzunluğu s = \sqrt{5^2 + 12^2} = 13 \text{ cm} bulunur.
  3. Alan (A): Eşkenar dörtgenin alanı, iki köşegenin çarpımının yarısıdır:
    A = \frac{10 \times 24}{2} = 120 \text{ cm}^2.
  4. Çevre ve Yarı Çevre: Kenar uzunluğu 13 cm olan bir eşkenar dörtgenin çevresi
    4 \times 13 = 52 \text{ cm},
    dolayısıyla yarı çevresi
    s = \frac{52}{2} = 26 \text{ cm}.
  5. Temas yarıçapı (r):
    r = \frac{A}{s} = \frac{120}{26} = \frac{60}{13} \text{ cm}.

Bu sebeple, bu şeklin içten teğet çemberinin yarıçapı 60/13 cm olarak elde edilir. Formülün temel mantığı, tangential (kenarlarına içten teğet) dörtgenlerde çemberin kenarlara dokunmasını sağlayan geometrik orantıya dayanmaktadır.

Özet Tablosu

Özellik Değer
Köşegenler (p ve q) 10 cm, 24 cm
Kenar Uzunluğu (s) 13 cm
Alan (A) 120 cm²
Çevre 52 cm
Yarı Çevre (s) 26 cm
Temas Yarıçapı (r = A / s) 60/13 cm

@simurg_yalcin