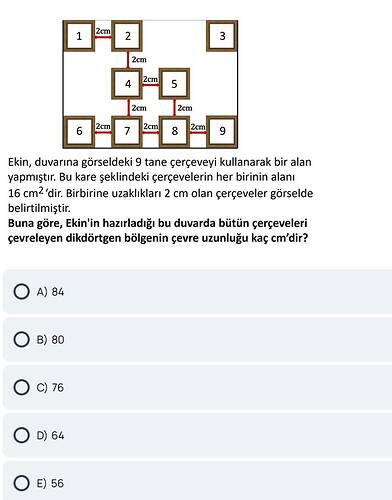
Buna göre, Ekin’in hazırladığı bu duvarda bütün çerçeveleri çevreleyen dikdörtgen bölgenin çevre uzunluğu kaç cm’dir?
Cevap:
Öncelikle her bir çerçevenin alanı 16 cm² olduğundan, çerçevelerin bir kenarı 4 cm’dir (çünkü 4 cm × 4 cm = 16 cm²). Görselden anlaşıldığı üzere çerçeveler, 3 satır halinde düzenlenmiştir:
- Üst satır: 1, 2, 3 numaralı çerçeveler
- Orta satır: 4, 5 numaralı çerçeveler
- Alt satır: 6, 7, 8, 9 numaralı çerçeveler
Her çerçevenin arası yatayda veya dikeyde 2 cm boşlukla gösterilmiştir.
1. Yatay (Genişlik) Hesabı
- Alt satırda 6, 7, 8, 9 olmak üzere 4 çerçeve vardır.
- Bu satırın yatayda kapladığı toplam genişlik:
- 4 çerçevenin toplam genişliği: 4 cm × 4 = 16 cm
- Bu 4 çerçeve arasında 3 boşluk vardır: 3 × 2 cm = 6 cm
- Yatay toplam: 16 cm + 6 cm = 22 cm
Üst veya orta satır ise daha az sayıda çerçeve içerdiğinden (3 ve 2 çerçeve) daha dar bir alan oluşturur. Dolayısıyla dikdörtgenin yatay boyutu 22 cm olarak belirlenir.
2. Dikey (Yükseklik) Hesabı
- Çerçeveler 3 satır hâlinde dizilidir (üst, orta, alt).
- Her satırda çerçeve yüksekliği 4 cm olduğundan, 3 satır toplamı: 3 × 4 cm = 12 cm
- Satırlar arasında 2 adet 2 cm boşluk vardır: 2 × 2 cm = 4 cm
- Dikey toplam: 12 cm + 4 cm = 16 cm
3. Dikdörtgenin Çevresi
Dikdörtgenin çevre formülü 2 × (genişlik + yükseklik) şeklindedir. Buna göre:
\text{Çevre} = 2 \times (22 + 16) = 2 \times 38 = 76 \text{ cm}.
Özet Tablo
| Ölçü | Hesaplama | Sonuç |
|---|---|---|
| Çerçeve kenar uzunluğu | 16 cm² alan ⇒ kenar = 4 cm | 4 cm |
| Yatayda toplam genişlik | (4 çerçeve×4 cm) + (3 boşluk×2 cm) | 16 cm + 6 cm = 22 cm |
| Dikeyde toplam yükseklik | (3 satır×4 cm) + (2 boşluk×2 cm) | 12 cm + 4 cm = 16 cm |
| Çevre | 2 × (22 + 16) | 76 cm |
Kısa Özet
• Her çerçevenin bir kenarı 4 cm, çerçeveler arası boşluk 2 cm’dir.
• En geniş satır (alt satır) 22 cm’ye, toplam yükseklik 16 cm’ye denk gelir.
• Dolayısıyla bütün çerçeveleri kaplayan dikdörtgenin çevresi 76 cm olarak bulunur.