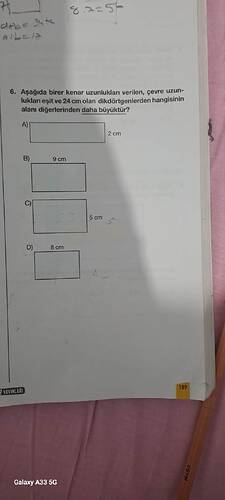
Aşağıda birer kenar uzunlukları verilen, çevre uzunlukları eşit ve 24 cm olan dikdörtgenlerden hangisinin alanı diğerlerinden daha büyüktür?
Verilen soru, çevresi 24 cm olan dikdörtgenlerin farklı bir kenar uzunluklarına göre alanlarının karşılaştırılmasını istemektedir. Dört farklı seçenek verilmiştir ve bu seçeneklerde bir dikdörtgenin bir kenarı verilmiştir. Diğer kenarı ise çevre formülüne göre hesaplanabilir.
Çevre formülünü hatırlayalım:
Çevre (C) = 2 * (uzun kenar + kısa kenar)
Dikdörtgenin çevresi 24 cm olduğuna göre:
24 = 2 \times (kısa\ kenar + uzun\ kenar)
Bu denklemi çözersek:
kısa\ kenar + uzun\ kenar = 12
Bu durumda kısa kenar ve uzun kenarı bulmak için verilen bir kenardan faydalanabiliriz. Her bir seçeneği hesaplayalım:
A Seçeneği:
- Verilen kenar: 2 cm
- Diğer Kenar: 12 - 2 = 10 cm
- Alan: 2 \times 10 = 20\ \text{cm}^2
B Seçeneği:
- Verilen kenar: 9 cm
- Diğer Kenar: 12 - 9 = 3 cm
- Alan: 9 \times 3 = 27\ \text{cm}^2
C Seçeneği:
- Verilen kenar: 5 cm
- Diğer Kenar: 12 - 5 = 7 cm
- Alan: 5 \times 7 = 35\ \text{cm}^2
D Seçeneği:
- Verilen kenar: 8 cm
- Diğer Kenar: 12 - 8 = 4 cm
- Alan: 8 \times 4 = 32\ \text{cm}^2
Sonuç olarak, C seçeneğindeki dikdörtgenin alanı diğerlerinden daha büyüktür, yani 35\ \text{cm}^2 ile en büyük alana sahiptir. Bu durumda doğru cevap C şıkkıdır.