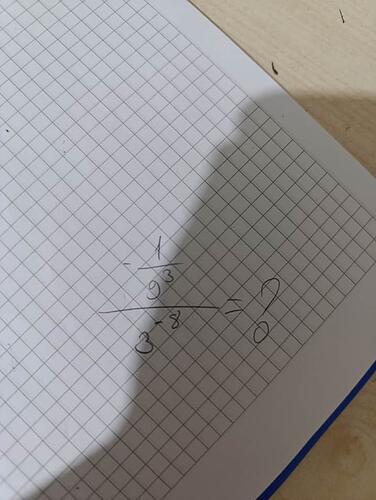Uslu İfadenin Çözümünü Bul
Verilen ifade:
$$\frac{\frac{1}{9^3}}{3^{-8}}$$
Bu ifadeyi adım adım çözelim.
1. Üstleri Hesaplama
A. Pay Kısmı:
9^3 ifadesi 9’un 3. kuvvetidir.
9’u, 3^2 olarak yazabiliriz, bu durumda:
$$(3^2)^3 = 3^{2 \times 3} = 3^6$$
Böylece:
$$\frac{1}{9^3} = \frac{1}{3^6} = 3^{-6}$$
B. Payda Kısmı:
3^{-8} ifadesi zaten açık durumda.
2. Üstlü Sayıların Bölümü
Genel kural: a^m / a^n = a^{m-n}
Bu durumda elimizde:
$$\frac{3^{-6}}{3^{-8}}$$
Bu da:
$$3^{-6 - (-8)} = 3^{-6 + 8} = 3^{2}$$
3. Sonuç
Sonuç olarak, ifade:
$$3^2 = 9$$
Bu nedenle, verilen uslu ifadenin çözümü 9’dur.
Bu adımlar, uslu sayıların anlaşılması ve uygulanmasında önemli kavramları içerir. Üstlerin toplanması ve çıkarılması kuralları, problemleri pratik bir şekilde çözmenizi sağlar.