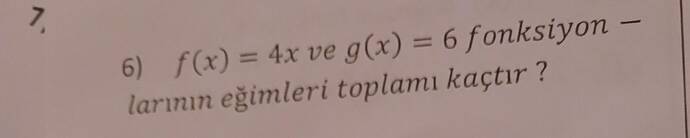Verilen fonksiyonların eğimleri toplamı kaçtır?
Temel Kavram
- Fonksiyonların eğimi, diferansiyel hesaplamada türev kullanılarak bulunur. Türev, bir fonksiyonun herhangi bir noktasındaki anlık değişim oranını, yani eğimini sağlar.
- Bir fonksiyonun türevi alındığında, fonksiyonun grafik üzerindeki eğimi elde edilir.
- Bir doğrusal fonksiyon olan f(x) = ax + b için eğim, direk katsayı a'dır.
Temel Yanıt
1. Adım: İpuçlarını Sunma
-
Fonksiyon 1: f(x) = 4x
- Bu fonksiyonun birinci dereceden yani doğrusal bir fonksiyon olduğunu fark ederiz.
- Eğimi, f(x) = ax formülündeki a katsayısıdır, burada a = 4.
-
Fonksiyon 2: g(x) = 6
- Bu fonksiyon sabit bir fonksiyondur ve grafiği, x eksenine paralel yatay bir doğrudur.
- Yatay bir doğrunun eğimi sıfırdır, yani burada eğim 0'dır.
2. Adım: Çıkarım Süreci
- Fonksiyon 1 için eğim 4.
- Fonksiyon 2 için eğim 0.
3. Adım: Çözümü Sonuçlandırma
- İki fonksiyonun eğimlerinin toplamını bulmak için eğimleri toplarız: 4 + 0.
Son Yanıt
- Verilen f(x) = 4x ve g(x) = 6 fonksiyonlarının eğimleri toplamı 4’tür.