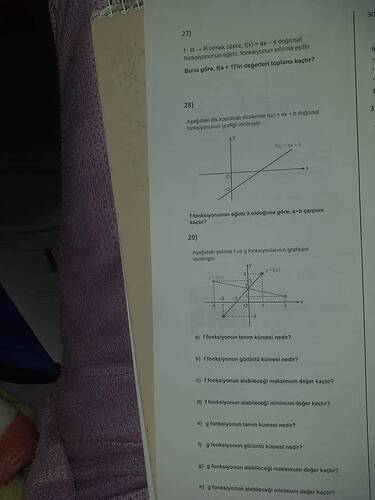
Görselde üç sorunun verildiği bir matematik testi yer almakta. Bunlardan ilki 27 numaralı soru olup, fonksiyonun eğimi üzerine. Test, verilen fonksiyonun eğimini ve sıfırını sormaktadır. Diğer sorular ise grafik yorumlama becerileriyle ilgili ve fonksiyonların tanım, görüntü kümeleri ile maksimum ve minimum değerlerini içermekte.
Detaylı bir çözüm için kısaca açıklayalım:
27. Soru:
Verilen fonksiyon f(x) = ax - 4 şeklindedir. Eğimi fonksiyonun sıfırına eşittir. f(a + 1) değerlerinin toplamını bulmak için öncelikle fonksiyonun eğimi olan a, fonksiyonun x-keseni ile kesiştiği noktada f(x) = 0 eşitliği sayesinde bulunabilir. Ardından yerine koyarak istenen toplam hesaplanabilir.
28. Soru:
Grafikte verilen doğrusal fonksiyonun eğimi 3’tür. Eğim formülü kullanılarak, a - b çarpımı hesaplanır.
29. Soru:
Fonksiyonların tanım ve görüntü kümeleri grafik üzerinden okunarak belirlenir. Grafikten fonksiyonların x ve y üzerindeki maksimum ve minimum değerleri gözlemlenebilir.
Bu tarz soru çözümlerinde grafik yorumları ve türev kavramları önemli olabilir. Başka soruların varsa sormaktan çekinme!
Cevapları nerde kerdeş
Tabii, soruların çözümlerini detaylı bir şekilde açıklayabilirim.
27. Soru Çözümü:
Verilen: f(x) = ax - 4 ve eğimi fonksiyonun sıfırına eşit.
Fonksiyonun eğimi a'dır. Fonksiyonun sıfırını bulmak için f(x) = 0 denklemini kullanırız:
$$ax - 4 = 0 \implies ax = 4 \implies x = \frac{4}{a}$$
Eğimi, yani a, bu sıfıra eşit olduğuna göre:
$$a = \frac{4}{a} \implies a^2 = 4 \implies a = \pm 2$$
İki olasılık var: a = 2 veya a = -2.
Şimdi f(a + 1)'i bulalım:
-
a = 2 için:
$$f(a + 1) = f(3) = 2 \cdot 3 - 4 = 6 - 4 = 2$$ -
a = -2 için:
$$f(a + 1) = f(-1) = -2 \cdot (-1) - 4 = 2 - 4 = -2$$
Değerlerin toplamı: 2 + (-2) = 0
Sonuç: f(a + 1) değerlerinin toplamı 0’dır.
28. Soru Çözümü:
Eğim 3 olarak verilmiş, bu durumda f(x) = 3x + b diyebiliriz.
Verilen grafik üzerinde, eğim noktalarından birine göre a - b çarpımı bulunmak isteniyor. Eğer doğru bir nokta ((x_1, y_1)) ve ((x_2, y_2)) ise:
$$\text{Eğim} = \frac{y_2 - y_1}{x_2 - x_1} = 3$$
3 eğim kullanılarak, farklı noktalardan hareketle a ve b değerleri belirlenebilir. Çözüm bu nedenle grafikteki özel noktalar üzerinden yapılmalıdır.
29. Soru Çözümü:
a) f fonksiyonunun tanım kümesi: Grafikte (x) ekseni boyunca hangi değerler var kontrol edilir.
b) f fonksiyonunun görüntü kümesi: Grafikte (y) ekseni boyunca hangi değerler var kontrol edilir.
c) f fonksiyonunun alabileceği maksimum ve minimum değer: Grafikte (f(x)) eğrisi üzerindeki en yüksek ve en düşük nokta tespit edilir.
d) f fonksiyonunun erişmediği değer: Tanım kümesi dışındaki (x) veya görüntü kümesi dışındaki (y) değerleri.
e ve f) g fonksiyonu için benzer adımlar: Tanım ve görüntü kümesi grafik üzerinden belirlenir.
Grafik üzerinden bu değerlere göz atmak ve fonksiyonları dikkatli değerlendirmek önemlidir. Yardımcı olabilirsem memnun olurum!