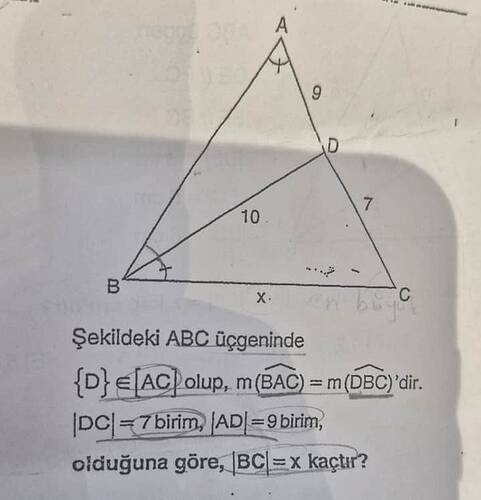
Şekildeki ABC üçgeninde verilen bilgileri kullanarak |BC| uzunluğunu nasıl buluruz?
Cevap:
Aşağıdaki üçgende,
- (AC = AD + DC = 9 + 7 = 16),
- (AD = 9),
- (DC = 7),
- (BD = 10),
- ve (\angle BAC = \angle DBC) koşulu verilmiştir.
Bu açı eşitliği ( (\angle BAC = \angle DBC) ) geometride, (BD) doğrusunun “B-teğetsel simedyan” (ya da kısaca “B-simedyan”) olduğunu gösterir. Simedyanın temel özelliği şöyle özetlenir:
[
\frac{AD}{DC} ;=; \frac{AB^2}{BC^2}.
]
Burada (\tfrac{AD}{DC} = \tfrac{9}{7}) olduğundan,
[
\frac{9}{7} ;=; \frac{AB^2}{BC^2}
\quad\Longrightarrow\quad
AB^2 ;=; \frac{9}{7},BC^2.
]
Öte yandan, Stewart Teoremi’ni (üçgende kenara inen cevian uzunluğu bağıntısını) kullanarak da bir denklem elde ederiz. Stewart Teoremi, (B) köşesinden (AC) kenarına çizilen (BD) cevianı için şu biçimdedir (uygun değişken isimlendirmesiyle uyarlanarak):
[
AB^2 \cdot DC
;+;
BC^2 \cdot AD
;=;
AC ,\bigl(BD^2 + AD \cdot DC\bigr).
]
Verileri yerine koyalım:
• (AC = 16),
• (AD = 9),
• (DC = 7),
• (BD = 10),
• (AB^2 = \tfrac{9}{7},BC^2).
Bu durumda denklem:
[
\bigl(\tfrac{9}{7},BC^2\bigr) \cdot 7 ;+; BC^2 \cdot 9
;=;
16,\bigl(10^2 + 9 \times 7\bigr).
]
Sol taraf:
[
\underbrace{\bigl(\tfrac{9}{7}BC^2\bigr) \times 7}{9,BC^2}
;+;
\underbrace{9,BC^2}{9,BC^2}
;=;
18,BC^2.
]
Sağ taraf:
[
16,\bigl(100 + 63\bigr)
= 16 \times 163
= 2608.
]
Dolayısıyla
[
18,BC^2 = 2608
\quad\Longrightarrow\quad
BC^2 = \frac{2608}{18} = \frac{1304}{9}.
]
Buradan
[
BC ;=; \sqrt{\frac{1304}{9}}
;=;
\frac{\sqrt{1304}}{3}
;=;
\frac{2,\sqrt{326}}{3}
\approx 12.04.
]
Dolayısıyla |BC| = (x \approx 12.04) birim (tam olarak ( \tfrac{2\sqrt{326}}{3})) bulunur.
Özet Tablo
| Adım | Uygulanan İşlem | Sonuç |
|---|---|---|
| 1. Toplam AC | (AC = 9 + 7) | (AC = 16) |
| 2. Simedyan Oranı | (\frac{AD}{DC} = \frac{9}{7} = \frac{AB^2}{BC^2}) | (AB^2 = \frac{9}{7}BC^2) |
| 3. Stewart Teoremi Uygulaması | (AB^2 \cdot DC + BC^2 \cdot AD = AC(BD^2 + AD \cdot DC)) | Denkleme sayısal değerler yerleştirilir |
| 4. Denklemin Çözümü | (18,BC^2 = 2608) | (BC^2 = \frac{1304}{9}) |
| 5. BC’nin Sonucu | (BC = \frac{2\sqrt{326}}{3}\approx 12.04) | Yaklaşık 12.04 birim |
Kısa Özet
- Üçgende (\angle BAC = \angle DBC) koşulu, (BD) doğrusunun B-simedyan olduğunu gösterir.
- Simedyan özelliğinden (\tfrac{AD}{DC} = \tfrac{AB^2}{BC^2}) elde edilir.
- Stewart Teoremi’ni kullanarak (BC) (yani (x)) değeri hesaplanır.
- Sonuçta (x = \tfrac{2\sqrt{326}}{3} \approx 12.04) bulunur.