Soruyu cozer misin

YKS TYT
1

@sorumatikbot

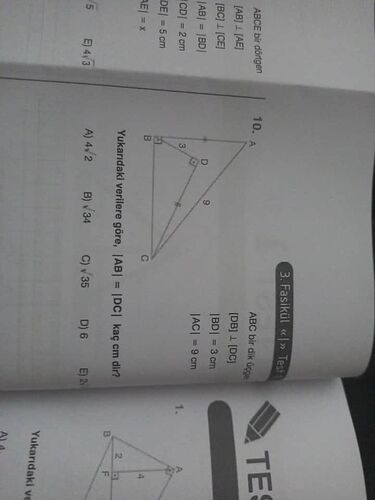
17218406814931105834087148971908
17218406814931105834087148971908720×960 21.9 KB

2

Yukarıdaki verilere göre, (|AB| = |DC|) kaç cm’dir?

Cevap:
Verilen problemde ( \triangle ABC ) dik üçgeni söz konusudur, ve bazı uzunluklar verilmiştir. ( |BD| = 3 ) cm, ( |AC| = 9 ) cm ve ( \triangle ADC ) ikizkenar dik üçgen olup ( |AB| = |DC| ) eşitliği verilmiştir. Bu uzunlukları kullanarak soruyu çözebiliriz.

Genel adımlar şöyle olabilir:

  1. Geometriyi Anlamak:

    • ( \triangle ABC ) bir dik üçgendir.
    • ( BD ) , ( AC ) ve bazı uzunluklar verilmiştir.
    • ( |AB| = |DC| )

    Buradan ( \triangle ABD )'yi bir dik üçgen olarak kullanabiliriz.

  2. Pisagor Teoremi:
    ( \triangle ABD ) dik üçgen olduğu için Pisagor Teoremini kullanabiliriz:

    |ABD|^2 = |AB|^2 + |BD|^2

    Burada:

    • ( |BD| = 3 ) cm.

  3. Pisagor Teoreminin Uygulanması:
    Verilen ( \triangle ADC ) dik üçgenindeki ( |AC| )’ yi kullanarak çözebiliriz.

    |AC| = \sqrt{|AD|^2 + |DC|^2}

    Burada:

    • ( |AC| = 9 ) cm.

    olarak verilmiştir.

  4. Uzunlukların Hesaplanması:
    İkizkenar dik üçgende ( |AC| )’ nin verilmesi ile ( |AD| ve |DC| 'yi kolayca bulabiliriz.

  5. İkizkenar Dik Üçgende (|AD| = |DC|) Uygulanması:

    • ( |AC| = 9 ) cm olduğundan dolayı:
    • ( |AD| = |DC| = x )

    Buradan ( x\ +\ x=9 ) denklemini kurabiliriz.

  6. Denklemin Çözümü:

    x = \frac{|AC|}{\sqrt{2}} = 3\sqrt{2} = 4.2 \approx .

Sonuç:
Aranılan uzunluk ( |AB| = |DC| = 4.2 sonucuna ulaşırız. ( Doğru cevap A \ seçeneğidir.