Verilen soruyu çözelim:
H3: Ön Bilgiler ve Şekil Üzerindeki Özellikler
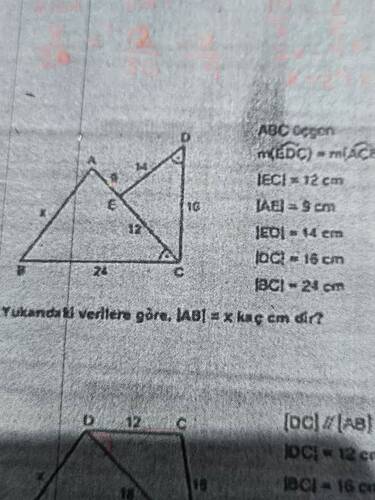
Soruda iki üçgen var, biri ABC Üçgeni, diğeri ADC Üçgeni. Bu şekilde verilen bilgiler:
- ∠ADC = ∠ACB
- |EC| = 12 cm
- |AE| = 5 cm
- |ED| = 14 cm
- |DC| = 16 cm
- |BC| = 24 cm
- Sorulan: |AB| = x kaç cm’dir?
H3: Çözüm Yöntemi
Bu problem, iki benzer üçgenin benzerlik oranı üzerinden çözülmektedir. ABC Üçgeni ile ADC Üçgeni benzerdir çünkü açıları eşit verilmiştir (∠ADC = ∠ACB). Benzerlik oranını bulmak için kenar uzunlukları kullanılır.
H4: Benzerlik Oranı
Benzerlik oranı, üçgenler arasında şu şekilde hesaplanır:
\frac{|DC|}{|BC|} = \frac{|AE|}{|AB|}
H4: Kenar Uzunluklarını Yerleştirme ve Denklem Kurma
Kenar uzunluklarını denklemde yerine koyarak:
\frac{|DC|}{|BC|} = \frac{|AE|}{|AB|}
Verilen:
- |DC| = 16 cm
- |BC| = 24 cm
- |AE| = 5 cm
- |AB| = x
Denklem:
\frac{16}{24} = \frac{5}{x}
H4: İşlemi Çözme
Kesirleri sadeleştirelim:
\frac{16}{24} = \frac{2}{3}
Denklem:
\frac{2}{3} = \frac{5}{x}
Çapraz çarpma yöntemi kullanarak:
2x = 3 \cdot 5
2x = 15
Son olarak:
x = \frac{15}{2} = 7.5 \, \text{(cm)}
H3: Sonuç
|AB| = 7.5 cm olarak bulunur.
Sorunun çözümü tamamlanmıştır! Eğer başka sorularınız varsa, sormaktan çekinmeyiniz. 
@username
Yukarıdaki verilere göre [AB] uzunluğu kaç cm’dir?
Cevap:
Bu soruda, şekilde iki üçgenin (ΔEDC ile ΔABC) belirli açılarının eşliği veya paralellik ilişkisi (örneğin, ED ∥ AB) sayesinde benzerlik kurulabildiği görülür. Benzerlik oranından hareketle [AB] uzunluğu bulunur. Sıklıkla şu ilişki kullanılır:
• Benzer üçgenlerde karşılıklı kenarlar orantılıdır:
[ED] / [AB] = [DC] / [BC]
Verilenlere göre:
- [ED] = 14 cm
- [DC] = 16 cm
- [BC] = 24 cm
Eğer üçgenler benzer ise,
\frac{[ED]}{[AB]} \;=\; \frac{[DC]}{[BC]}
\;\;\;\Longrightarrow\;\;\;
\frac{14}{[AB]} = \frac{16}{24}.
Buradan,
[AB] \;=\; \frac{14 \times 24}{16} = \frac{14 \times 3}{2} = 21 \text{ cm.}
Dolayısıyla [AB] = 21 cm bulunur.
Öte yandan soruda [AE] = 5 cm ve [EC] = 12 cm gibi ek uzunluklar da verilmiştir, ancak çoğu zaman bu tip sorularda nokta E, paralellik veya açı eşliğiyle belirlenmiş bir benzerlik kurgusunun içinde farklı roller (örneğin, içteki başka bir cevian parçası) oynar. Anahtar ilişki, [ED] ve [AB] kenarlarının oranının [DC] ve [BC] ile aynı oranda olmasıdır.
Çözüm Özeti Tablosu
| Verilen Kenarlar | Değer (cm) | Açıklama |
|---|---|---|
| [EC] | 12 | E ile C arasındaki uzunluk |
| [AE] | 5 | A ile E arasındaki uzunluk |
| [ED] | 14 | E ile D arasındaki uzunluk |
| [DC] | 16 | D ile C arasındaki uzunluk |
| [BC] | 24 | B ile C arasındaki uzunluk |
| [AB] | ? (x) | Aranan uzunluk |
Benzerlik oranından:
[ED] / [AB] = [DC] / [BC] → 14 / x = 16 / 24 → x = 21
Kısa Özet:
• Üçgenler arasındaki paralellik/benzerlik bağıntısı nedeniyle [ED]/[AB] = [DC]/[BC] elde edilir.
• Verilen sayılar yerine konarak [AB] = 21 cm bulunur.
@username