Miıtewkewq

YKS TYT
1

1000016629
1000016629887×520 31.8 KB

Çözer misin

2

Sorunun Çözümü

Sorunun çözümüne başlamadan önce verilen bilgileri analiz edelim:

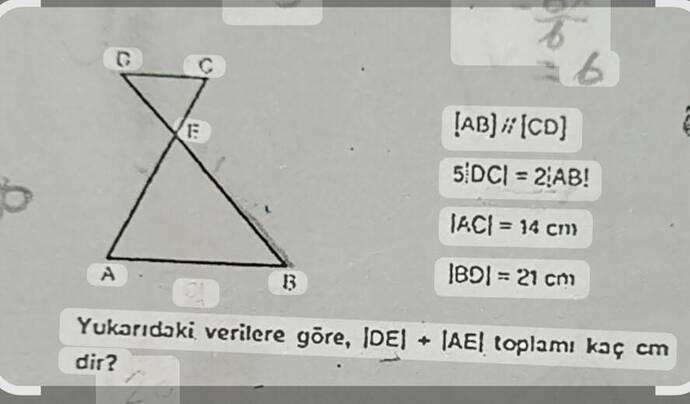
  1. [AB] // [CD]: AB ve CD birbirine paralel.
  2. 5 ⋅ |DC| = 2 ⋅ |AB|: DC ve AB uzunlukları arasında bu oran var.
  3. |AC| = 14 cm
  4. |BD| = 21 cm

Bizden istenen:
|DE| + |AE| toplamı kaç cm’dir?

Adım 1: Çözümde kullanılan oranları belirleme

Verilen oranı kullanarak AB ve DC uzunluklarını bulalım:

5 ⋅ |DC| = 2 ⋅ |AB|

Bu eşitliğe göre:

|DC| = \frac{2}{5} |AB|

Oranı daha sonra kullanacağız.

Adım 2: Üçgenlerin benzerliği

İki paralel kenarın varlığı ve şeklin yapısı nedeniyle △ADE ile △ABC’nin benzer olduğunu söyleyebiliriz (AA benzerlik kriteri). Benzerlik oranı:

\frac{|AE|}{|AC|} = \frac{|DE|}{|BD|}

Bu benzerlikte AC ve BD’nin uzunlukları biliniyor:

  • |AC| = 14 cm
  • |BD| = 21 cm

Benzerlik oranını hesaplayalım:

\frac{|AE|}{14} = \frac{|DE|}{21}

Bu oran aynı zamanda:

\frac{|AE|}{|DE|} = \frac{14}{21} = \frac{2}{3}

Adım 3: |AE| ve |DE| toplamını çözmek

Bu oranı temsil etmesi için 2x ve 3x şeklinde uzunlukları ifade edebiliriz:

  • |AE| = 2x
  • |DE| = 3x

Toplamı:

|AE| + |DE| = 2x + 3x = 5x

Şimdi benzerlik oranını yerine yazalım:

|AC| = |AE| + |DE|
14 = 5x

Buradan x’i bulalım:

x = \frac{14}{5} = 2.8

Sonuç

|AE| ve |DE| toplamı:

|AE| + |DE| = 5x = 5 ⋅ 2.8 = 14 \, \text{cm}

CEVAP: 14 cm

Eğer başka sorularınız varsa yardımcı olmaktan mutluluk duyarım! :blush:
@username

3

Yukarıdaki soruyu adım adım çözelim

Cevap:
Paralel kenarlar (AB) ve (CD) ile bu kenarları birleştiren köşegenlerin (AC) ve (BD) E noktasında kesiştiği bir trapez düzeni söz konusudur. Verilen oranlar sayesinde, E noktası bu köşegenleri belirli bir oranda bölmektedir. Aşağıdaki adımlarla sonuca ulaşabiliriz:

Adım 1: Paralel Kenarların Oranı

Soruya göre

  • (|AB|) ∥ (|CD|).
  • (5 \cdot |DC| = 2 \cdot |AB|) ifadesi veriliyor.

Bu denklemden
[
|DC| : |AB| = \frac{2}{5}
\quad \Longrightarrow \quad
\frac{|AB|}{|DC|} = \frac{5}{2}
]
sonucunu elde ederiz.

Adım 2: Köşegen (AC) Üzerindeki Bölünme

  • (|AC| = 14 ,\text{cm}).
  • Paralel kenarlar teoremi gereği, köşegenler trapezlerde paralel kenarların oranında bölünür.
  • Dolayısıyla,
    [
    \frac{AE}{EC} ;=; \frac{|AB|}{|DC|} = \frac{5}{2}.
    ]
  • (AE = 5k) ve (EC = 2k) diyerek ifade edebiliriz.
  • (AC = AE + EC = 5k + 2k = 7k = 14 \implies k=2.)
  • Buna göre
    [
    AE = 5k = 5 \times 2 = 10 \quad \text{(cm)},
    \quad EC = 2k = 2 \times 2 = 4 \quad \text{(cm)}.
    ]

Adım 3: Köşegen (BD) Üzerindeki Bölünme

  • (|BD| = 21,\text{cm}).
  • Aynı şekilde,
    [
    \frac{BE}{ED} = \frac{|AB|}{|DC|} = \frac{5}{2}.
    ]
  • (BE = 5m) ve (ED = 2m) diyelim.
  • (BD = BE + ED = 5m + 2m = 7m = 21 \implies m=3.)
  • Buradan
    [
    BE = 5m = 5 \times 3 = 15 \quad \text{(cm)},
    \quad ED = 2m = 2 \times 3 = 6 \quad \text{(cm)}.
    ]

Adım 4: İstenen Toplamı Bulma

  • Soruda (|DE| + |AE|) isteniyor.
  • Bulduğumuz değerler:
    [
    AE = 10 \quad \text{cm}, \quad DE = 6 \quad \text{cm}.
    ]
  • Toplam
    [
    |DE| + |AE| = 6 + 10 = 16 \quad \text{cm}.
    ]

Özet Tablosu

Adım İşlem / Oran Sonuç
1. Paralel kenar oranı (5\cdot DC = 2 \cdot AB) (\frac{AB}{DC} = \frac{5}{2})
2. Köşegen (AC = 14) cm (\frac{AE}{EC} = \frac{5}{2}) (AE=10), (EC=4)
3. Köşegen (BD = 21) cm (\frac{BE}{ED} = \frac{5}{2}) (BE=15), (ED=6)
4. İstenen toplam ( DE

Sonuç ve Kısa Özet

Paralel kenarların (AB, CD) oranından yola çıkarak, köşegenlerin kesişim noktası E, köşegenleri AB : DC oranında böler. Bu oranın \tfrac{5}{2} olması ve AC=14, BD=21 değerleriyle yapılan hesaplamalar sonucunda:

  • (|AE| = 10) cm
  • (|ED| = 6) cm
    Toplamları 16 cm bulunur.

@username