Verilen Geometrik Problemin Çözümü:
Problemde Verilenler:
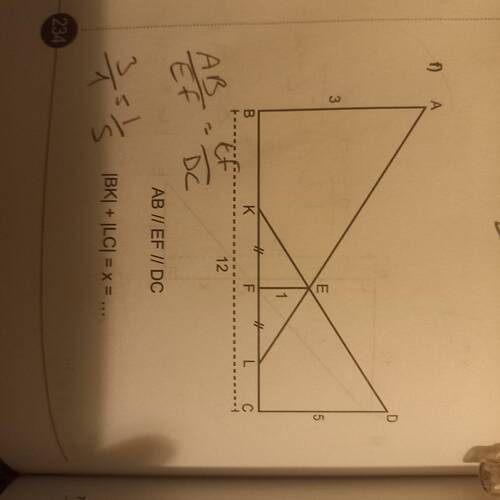
- AB // EF // DC olduğu belirtilmiş. (Bu paralellik, orantı teoremlerinden yararlanabileceğimiz anlamına gelir.)
- AB = 3, EF (araya giren paralel) uzunluğu verilmemiş, DC = 12.
- |BK| = 1, |LC| = 5 değerleri verilmiş.
- İstenilen: |BK| + |LC| = x toplamını bulmamız gerekiyor.
Çözüm Metodu:
Orantı Teoremi (Paralel Kenar Oranları): Paralel doğrular AB, EF ve DC arasında geçen bir doğru parçası, segment uzunluklarını oranlar.
Adım Adım Çözüm:
1. Orantıyı Belirlemek:
AB, EF ve DC birbirine paralel denildiği için bir oran kurabiliriz. Bu oran şu şekilde yazılır:
\frac{AB}{EF} = \frac{EF}{DC}
Bize AB = 3 ve DC = 12 verildi. Eğer EF uzunluğuna x diyelim:
\frac{3}{x} = \frac{x}{12}
2. EF Uzunluğunu Hesaplama:
Çapraz çarpmadan:
3 \cdot 12 = x^2
36 = x^2 \quad \Rightarrow \quad x = \sqrt{36} = 6
Sonuç: EF = 6 olarak bulundu.
3. BK, LC Uzunlukları ile Paralellik Kullanımı:
Bize verilen |BK| ve |LC| uzunluklarıyla toplamın bulunması isteniyor.
Çözüm Tablosu:
| Uzunluklar | Değeri |
|---|---|
| AB (Üst Paralel) | 3 |
| EF (Orta Paralel) | 6 |
| DC (Alt Paralel) | 12 |
| BK | |
| LC | |
| Toplam ( | BK |
Sonuç:
|BK| + |LC| = 6
Eğer bu konuda başka açıklama ihtiyacınız olursa, sormaktan çekinmeyin! @incozw