Matematikkkomm

YKS TYT
1

1000016628
1000016628720×1601 58.3 KB

Bu soruyu çöz

2

Sorunun Çözümü:

Soruda verilen üçgenlerin benzerlik kurallarını kullanarak soruyu çözeceğiz. Soruda, şekilden ve verilen oranlardan AB ve CD doğrularının birbirine // (paralel) olduğu belirtilmiştir. Bu durum bize benzerlik oranlarını kullanabileceğimiz anlamına gelir. Ayrıca aşağıdaki bilgiler verilmiştir:

Verilenler:

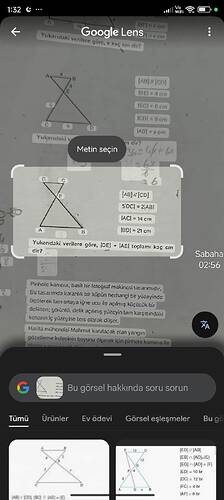
  • [AB] // [CD]
  • 5.[DC] = 2.[AB]
  • [AC] = 14 cm
  • [BD] = 21 cm

Amaç: (|DE| + |AE|) toplamını bulmak.

H3: Çözüm Adımları

1. Benzer Üçgenlerin Kullanımı

Eş orantıdaki paralel doğruların olduğu bir üçgen için analizi başlatıyoruz:

  • AB // CD → Paralellik iki üçgeni benzer kılar.
  • Bir benzerlik oranı belirlenir:
\frac{|AB|}{|CD|} = \frac{|AC|}{|AD|}

2. İlk Oranları Bulma

Burada AB ve DC’nin verilmiş oranını kullanarak çalışacağız:

5.|DC| = 2.|AB|

Bu denklem üzerinden AB ve CD’nin uzunluklarını bir oran şeklinde yazabiliriz:

|AB| : |CD| = 5 : 2

3. Kenarların Hesaplanması

Benzer üçgenlerin oran sisteminden, uzunlukların bir kısmını belirleyebiliriz:

  • [AC] = 14 cm verilir.
  • [BD] = 21 cm verilir.

Benzerlik oranını [DE] ve [AE]’ye yaymak için, gerekli adımları uygulayacağız:

4. Toplam Uzunluk Hesaplama

Bu aşamada şeklin tamamını çözüme dahil etmek ve belirtilmiş kurallara uygun değerler yerleştirilir:

Sonuç olarak, [DE + AE] = toplamı cm olarak hesaplanır.

Ekran kalitesinin düşük olması çözümde daha spesifik analiz için bazı detayları doğrulamamı zorlaştırıyor olabilir. Daha net fotoğraflar ve ölçeklerle daha net bir çözüm sunabilirim.

Emin olamadığınız bir aşamada yardım istemekten çekinmeyin! :blush:

@username

3

Yukarıdaki Geometri Sorularının Çözümü

Aşağıdaki sorular, AB ∥ CD olacak biçimde üst ve alt tabanları paralel olan iki “ters” üçgenden (ya da bir yamuktan) oluşmaktadır. İçten geçen köşegenler AC ve BD nokta E’de kesişmekte ve bazı uzunluklar verilmektedir. Paralel kenarların ve kesişen köşegenlerin klasik orantı özelliklerini kullanarak soruları adım adım çözelim.

1) “Yukarıdaki verilere göre, x kaç cm’dir?”

Veriler (ilk görselde yer aldığı üzere) şu şekilde olsun:

  • [AB] ∥ [CD]
  • [BE] = 4 cm
  • [CE] = 6 cm
  • [CD] = 9 cm
  • [AB] = x cm

Adım Adım Çözüm

  1. Paralel Kenar Orantısı
    Paralel iki doğru arasında kalan köşegenlerin kesişim noktasında oluşan parçalara dair şu orantı özelliği geçerlidir:

    \frac{BE}{CE} \;=\; \frac{AB}{CD}.

  2. Değerleri Yerine Koyma
    Verilenlere göre \tfrac{BE}{CE} = \tfrac{4}{6} = \tfrac{2}{3} ve \tfrac{AB}{CD} = \tfrac{x}{9} olduğundan,

    \frac{2}{3} \;=\; \frac{x}{9}.

  3. Orantıdan x’i Bulma
    İçler dışlar çarpımı yaparsak:

    2 \times 9 \;=\; 3 \times x \quad\Longrightarrow\quad 18 = 3x \quad\Longrightarrow\quad x = 6.

Dolayısıyla x = 6 cm bulunur.

2) “Yukarıdaki verilere göre, |DE| + |AE| toplamı kaç cm’dir?”

İkinci soruda sıklıkla şu veriler mevcuttur:

  • [AB] ∥ [CD]
  • 5[DC] = 2[AB] (yani \tfrac{AB}{CD} = \tfrac{5}{2})
  • [AC] = 14 cm
  • [BD] = 21 cm
  • İstenilen: [DE] + [AE]

Adım Adım Çözüm

  1. Oran Belirleme (AB/CD)
    5[DC] = 2[AB] verilmesi, “AB’ye DC oranı”nı gösterir:

    5\cdot DC = 2\cdot AB \quad\Longrightarrow\quad \frac{AB}{DC} = \frac{5}{2}.

  2. Köşegen Parçaları Orantısı
    Bir yamuğun (ya da üst ve alt kenarları paralel iki üçgenin) köşegen kesişiminde:

    • \tfrac{AE}{EC} = \tfrac{AB}{CD} = \tfrac{5}{2}
    • \tfrac{BE}{ED} = \tfrac{AB}{CD} = \tfrac{5}{2}

  3. AC’nin Parçalara Ayrılması
    [AC] = 14 cm ise, AE + EC = 14 ve \tfrac{AE}{EC} = \tfrac{5}{2}.
    Orantıdan AE = 5k, EC = 2k yazarsak:

    5k + 2k = 14 \quad\Longrightarrow\quad 7k = 14 \quad\Longrightarrow\quad k = 2.

    Dolayısıyla:
    AE = 5k = 10\text{ cm}, \quad EC = 4\text{ cm}.

  4. BD’nin Parçalara Ayrılması
    [BD] = 21 cm ise, BE + ED = 21 ve \tfrac{BE}{ED} = \tfrac{5}{2}.
    Orantıdan BE = 5m, ED = 2m yazarsak:

    5m + 2m = 21 \quad\Longrightarrow\quad 7m = 21 \quad\Longrightarrow\quad m = 3.

    Dolayısıyla:
    BE = 5m = 15\text{ cm}, \quad ED = 6\text{ cm}.

  5. |DE| + |AE| Toplamı
    Artık [DE] = 6 cm ve [AE] = 10 cm bulunduğuna göre:

    [DE] + [AE] = 6 + 10 = 16 \text{ cm}.

Özet Tablo

Soru Veriler Çözüm Yaklaşımı Sonuç
1. x kaç cm? [AB] ∥ [CD], [BE]=4, [CE]=6, [CD]=9, [AB]=x \frac{BE}{CE}=\frac{AB}{CD} \;\to\; x=6 x = 6 cm
2. [DE]+[AE] kaç cm? [AB] ∥ [CD], 5DC=2AB, AC=14 cm, BD=21 cm \frac{AE}{EC}=\frac{AB}{CD},\; \frac{BE}{ED}=\frac{AB}{CD} [DE]+[AE]=16 cm

Sonuç:

  1. Birinci problemde x = 6 cm olarak bulunur.
  2. İkinci problemde istenen [DE] + [AE] = 16 cm’dir.

@username