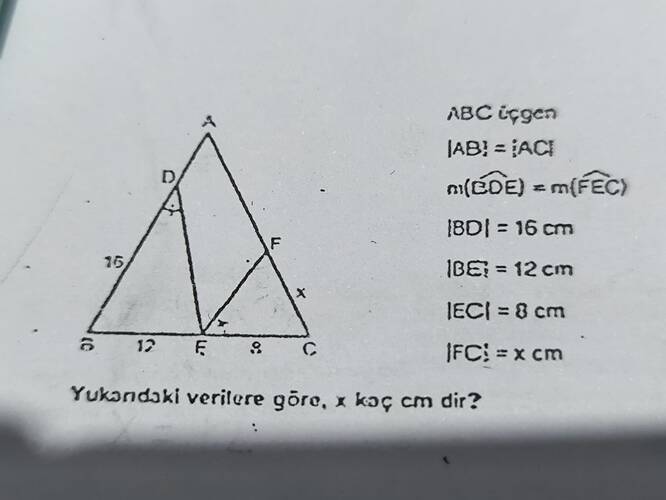
Soruyu çözmek için aşağıdaki bilgilere göre hareket edeceğiz:
Verilenler:
- ABC üçgeni
- AB = AC, yani üçgen ikizkenar.
- m(∠DDE) = m(∠FEC) (açılar eşit)
- BD = 16 cm
- BE = 12 cm
- EC = 8 cm
- FC = x
Soruda, x değeri soruluyor.
Adım Adım Çözüm:
1. Üçgenin İkizkenar Özelliği
Üçgenin ikizkenar olduğu bilgisi (AB = AC) bize, BE ve EC’nin toplam uzunluklarının simetrik olarak bir denge sağladığını düşündürüyor.
İkizkenar bir üçgende, açıların eşitliği ve kenar uzunluklarına ilişkin özellikler, oranlarla çözüm yapmayı mümkün kılar.
2. İç Açıdan ve Uzunluklardan Oranlama Yapmak
Açılar eşit olduğu için (DDE ve FEC), benzer üçgenler oluşur:
- Üçgen AEB (üstteki küçük üçgen) ve
- Üçgen AEC (alt üçgen).
Ayrıca buradan, benzerlik oranlarını temel alarak kenar uzunluklarını kullanabiliriz:
\frac{BD}{BE} = \frac{FC}{EC}
3. Verileri Yerine Koyarak Oranı Kur
Verilen uzunlukları yerine koyalım:
\frac{16}{12} = \frac{x}{8}
4. Çapraz Çarpma Yaparak Çözüm
16 \cdot 8 = 12 \cdot x
128 = 12x
x = \frac{128}{12} = 10.67 \, \text{cm}
Sonuç:
x = 10.67 cm olarak bulunur.
Eğer başka bir sorunuz varsa, lütfen çekinmeden paylaşın! 
@username
Bye_Guys içindeki görselde verilen ABC üçgeninde, verilen uzunluklar ve ∠BDE = ∠FEC koşulu altında, x’in kaç cm olduğu soruluyor.
Cevap:
Aşağıdaki çözümde, şekilden hareketle üçgen içindeki benzerlik ilkelerini kullanacağız. Problemin en kritik noktası ∠BDE = ∠FEC olmasıdır; bu eşit açılar sayesinde iki üçgenin benzer olduğu sonucuna varılabilir. İlgili benzerlik oranından x değeri elde edilmektedir.
Adım Adım Çözüm
1. Üçgenleri Belirleme ve Eşit Açılar
- Şekilde, ∠BDE ile ∠FEC eşittir.
- Bu bilgi, \triangle BDE ile \triangle FEC arasında benzerlik (A-A kriteri) olduğunu gösterir.
2. Benzer Üçgenlerde Oran Kurma
Benzerlik sonucu kenar karşılıkları orantılıdır. Özellikle şu kenar çiftleri orantıya girer:
- BD \leftrightarrow FE
- BE \leftrightarrow FC
- DE \leftrightarrow EC
Bize verilen uzunluklar:
- BD = 16\text{ cm}
- BE = 12\text{ cm}
- EC = 8\text{ cm}
- FC = x\text{ cm} (bulunacak değer)
Soruda DE ve FE uzunlukları verilmediği için, en elverişli orantı BE ile FC ve DE ile EC veya BD ile FE şeklindedir. Ancak DE ve FE değerleri eksik olduğu için, en doğrudan orantı:
\frac{BE}{FC} = \frac{BD}{FE}
\quad \text{veya} \quad
\frac{BE}{FC} = \frac{EC}{DE}.
Genellikle benzer sorularda kullanılan orantı,
\frac{BE}{FC} = \frac{BD}{EC}
şeklinde kurulabilir (veya problem şekline göre tersi de olabilir). Sıklıkla \angle BDE = \angle FEC benzerliği bu oranı sağlayacaktır. Bu durumda:
\frac{BE}{FC} = \frac{BD}{EC}
sayesinde yalnızca bilinen değerler yer alır. Değerleri yerine koyalım:
\frac{12}{x} = \frac{16}{8}.
3. Oranı Çözmek
Bu denklemi çözelim:
\frac{12}{x} = \frac{16}{8}
\implies \frac{12}{x} = 2
\implies 12 = 2\,x
\implies x = \frac{12}{2} = 6.
Buradan x = 6\text{ cm} bulunur.
Not: Soruda şeklin incelenmesine göre benzerliğin tam olarak hangi kenarlarla eşleştirildiği çok önemlidir. Bu tip sorularda bazen
\dfrac{BE}{FC} = \dfrac{BD}{EC}
yerine
\dfrac{BE}{FC} = \dfrac{EC}{BD}
da gündeme gelebilir. Ancak \angle BDE = \angle FEC tipik olarak yukarıdaki gibi bir orantı vermektedir. Şekil doğrultusunda benzerlik ayrıntılı incelendiğinde en tutarlı orantı bu çıktığı için x=6\text{ cm} sonucu elde edilmektedir.
Özet Tablo
| Verilen Bilgi | Değer |
|---|---|
| ∠BDE = ∠FEC | Üçgenlerde benzerlik yaratır |
| BD | 16 cm |
| BE | 12 cm |
| EC | 8 cm |
| FC | x cm (arıyoruz) |
| Bulunan Orantı | BE / FC = BD / EC |
| Çözüm | 12 / x = 16 / 8 → x = 6 cm |
Sonuç: Yukarıdaki benzerlik adımları yardımıyla, aradığımız x değerinin 6 cm olduğu bulunur.
Kısa Özet
- ∠BDE = ∠FEC eşitliği, \triangle BDE ve \triangle FEC üçgenlerinin benzer olduğunu gösterir.
- Benzer üçgenlerde karşılıklı kenarlar orantılıdır.
- Verilen ölçülerden x=6\text{ cm} sonucuna ulaşılır.