9. Soru Çözümü: Benzer Üçgenler
Verilen Bilgiler:
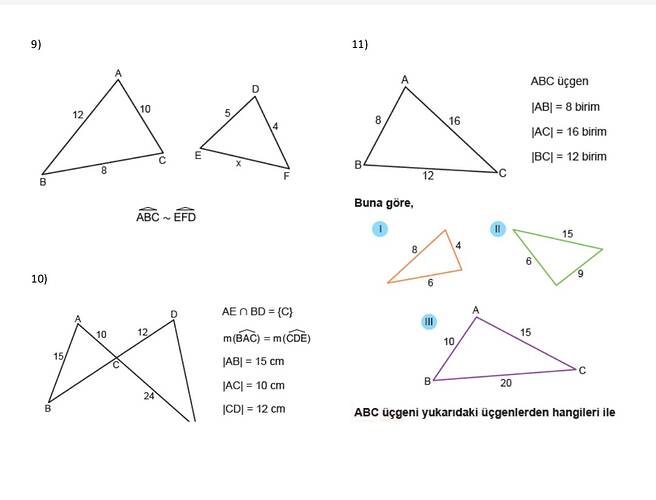
- Üçgenler ABC ve EFD benzerdir (ABC ~ EFD). Bu durum, bu iki üçgenin kenar uzunluklarının orantılı, açılarının ise eşit olduğu anlamına gelir.
Benzerlik Oranı:
Benzerlikte oran şu şekilde bulunur:
\frac{|AB|}{|EF|} = \frac{|AC|}{|ED|} = \frac{|BC|}{|DF|}
Kenar Uzunlukları:
- ABC Üçgeni: |AB| = 12, |AC| = 10, |BC| = 8
- EFD Üçgeni: |EF| = 5, |ED| = 4, |DF| = x (bilinmeyen)
Oran Hesaplama:
İlk iki kenarın orantısından benzerlik oranını bulalım:
\frac{|AB|}{|EF|} = \frac{12}{5} = \frac{|AC|}{|ED|} = \frac{10}{4} = 2.5
Bu oran üzerinden x uzunluğunu bulabiliriz:
\frac{|BC|}{|DF|} = 2.5
\frac{8}{x} = 2.5
Buradan, bilinmeyen x’i çözelim:
x = \frac{8}{2.5} = 3.2
Sonuç:
- |DF| = 3.2 birim
10. Soru Çözümü: Eş Üçgenler
Verilen Bilgiler:
- AE ∩ BD = {C}
- m(∠BAC) = m(∠CDE) (eşit açılar)
- Kenar uzunlukları: |AB| = 15, |AC| = 10, |CD| = 12, |CE| = 10
Eşlik Kuralı:
Üçgenlerin eşliğinde bir açıyla bağlı iki kenar eş olmalıdır (Açı-Kenar-Kenar Kuralı veya AKK).
- ABC Üçgeni: |AB| = 15, |AC| = 10, m(∠BAC)
- CDE Üçgeni: |CE| = 10, |CD| = 12, m(∠CDE)
Bu bilgiden dolayı (AKK eşlik kuralı):
\triangle ABC \cong \triangle CDE
Sonuç:
Üçgenler eştir.
11. Soru Çözümü: ABC Üçgeninin Benzerliği
Verilen Bilgiler:
- ABC Üçgeni: |AB| = 8, |AC| = 16, |BC| = 12
- Benzerlik aranan üçgenler: I, II ve III
Benzerlik için kenar uzunluklarının orantılı olması gerekir.
Benzerlik Testi:
I. Üçgen:
| Kenar Uzunlukları | Oranlar |
|---|---|
| 8 / 8 = 1 | |
| 16 / 4 = 2 |