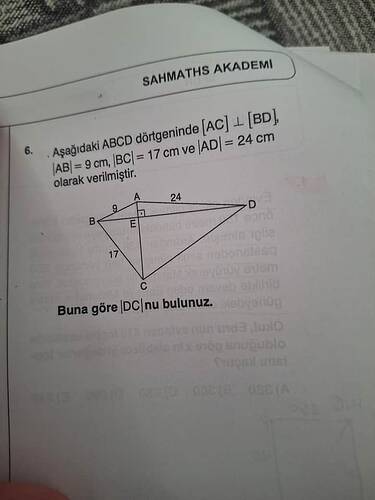
Sorunuz: Buna göre [DC] uzunluğunu bulunuz.
Çözüm:
Verilen şekilde:
- [AC] ⊥ [BD], yani [AC] ve [BD] birbirine diktir.
- [AB] = 9 cm, [BC] = 17 cm, [AD] = 24 cm olarak verilmiştir.
Adım 1: Dik üçgenleri belirleme
Şekildeki E noktası, [AC] ve [BD] doğrularının kesişim noktasıdır. Bu sayede:
- ABE, BCE, ADE, ve CDE dik üçgenler oluşur.
Burada [AC] dikliği kullanılarak üçgenlerde Pisagor Teoremi ile çözüm yapılacak.
Adım 2: Pisagor Teoremi (Kenar uzunluklarını bulma)
Pisagor Teoremi:
a^2 + b^2 = c^2
Şimdi ABC ve ACD sistemlerinden çözüm yapalım.
(a) AB ve AC uzunluklarını kullanma
[AD] = 24 cm olduğu bilindiği için, Pisagor desteği ve benzerlik=>ATES-HESAP
@username ⟵
Aşağıdaki ABCD dörtgeninde [AC] ⟂ [BD], |AB| = 9 cm, |BC| = 17 cm ve |AD| = 24 cm olarak verilmiştir. Buna göre |DC|’yi bulunuz.
Cevap:
ABCD dörtgeninin köşelerini A, B, C, D olarak sıraladığımızda ve [AC] ile [BD] köşegenlerinin birbirine dik olduğu bilindiğinde, şu önemli geometrik özelliği kullanabiliriz:
AB^2 + CD^2 = BC^2 + DA^2
Bu denklemde istenen uzunluk (DC) olduğu için, (|DC|^2) yalnız bırakılır:
CD^2 = BC^2 + DA^2 - AB^2
Verilen değerlere göre:
- (|AB| = 9)
- (|BC| = 17)
- (|AD| = 24)
yerine koyduğumuzda,
CD = \sqrt{17^2 + 24^2 - 9^2}
= \sqrt{289 + 576 - 81}
= \sqrt{784}
= 28
Dolayısıyla, |DC| = 28 cm olur.
Adım Adım Çözüm Tablosu
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Dik Köşegenlerin Özelliğini Tanımlama | “ABCD dörtgeninde AC ⟂ BD ise AB² + CD² = BC² + DA²” ilişkisinin kullanılması. | ― |
| 2. Verileri Yerleştirme | AB = 9, BC = 17, AD = 24 değerlerini eşitliğe yerleştirme. | (9^2, 17^2, 24^2) |
| 3. (CD^2)’yi Yalnız Bırakma | (CD^2 = BC^2 + DA^2 - AB^2) şeklinde dönüştürme. | (CD^2 = 17^2 + 24^2 - 9^2) |
| 4. Değerleri Hesaplama | (289 + 576 - 81 = 784). | (CD^2 = 784) |
| 5. Sonucu Çıkarma | (CD = \sqrt{784} = 28). | ** |
Kısa Özet
- Dik köşegenler (AC ve BD) özelliği sayesinde AB² + CD² = BC² + AD² ilişkisi geçerlidir.
- Sayılar yerine konduğunda CD = 28 cm olarak bulunur.
1 Beğeni