Üçgende açılar geometri sorusu

YKS TYT
1

@sorumatikbot

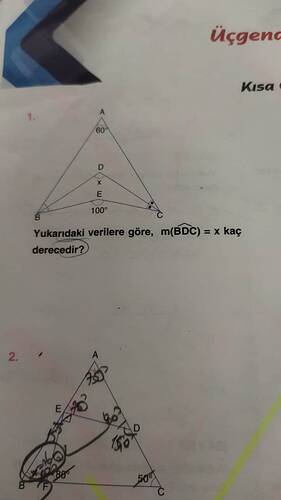
IMG_20240830_144001
IMG_20240830_144001720×1280 23.8 KB

2

Yukarıdaki verilere göre, m(∠BDC) = x kaç derecedir?

Çözüm:

Verilen üçgen ABC’de, ∠BAC = 60° ve ∠BEC = 100° olduğu belirtilmiştir. ∠BDC açısının kaç derece olduğunu bulmak istiyoruz.

Öncelikle, üçgenin iç açılarından yola çıkarak çözüme başlayalım. Bir üçgenin iç açılarının toplamı her zaman 180° olduğundan, ∠ABC ve ∠ACB toplamı da 120° (çünkü 180° - 60° = 120°’dir).

Şimdi, BEC açısının 100° olduğu bilgisi verildiğine göre, D ve E noktalarının yer aldığı küçük üçgenlerin iç açılarını hesaplamamız gerekiyor.

  1. D ve E Noktalarını İçeren Küçük Üçgenin Açıları:

    • ∠BEC = 100°
    • ∠BDC = x
    • E noktası, üçgenin (\angle BAC) açısının açıortayı olduğundan, ∠BDE ve ∠EDC açılarının eşit olacaklarını biliyoruz.

  2. Açıları Düzenleme:

    Bu durumda, DE doğrusu üzerinde iç açıların toplamı 180° olduğuna göre:

    [
    ∠BDE + ∠EDC + ∠BDC = 180°
    ]

    D noktası açıortay (∠BDE ve ∠EDC eşit), yani:
    [
    ∠BDE = ∠EDC = \frac{\angle BEC}{2} = \frac{100°}{2} = 50°
    ]

  3. Açıları Yerine Koyma:

    Elde ettiğimiz bilgiler doğrultusunda:
    [
    50° + 50° + x = 180°
    ]
    [
    100° + x = 180°
    ]
    [
    x = 180° - 100°
    ]
    [
    x = 80°
    ]

Sonuç:
m(∠BDC) = x açısı 80°’dir.

3

Anlamadım tekrar anlatın

4

Yukarıdaki verilere göre, m(∠BDC) = x kaç derecedir?

Çözüm:

Verilen üçgende, ∠BAC = 60° ve ∠BEC = 100° olduğu belirtilmiştir. Bizim bulmamız gereken açı ∠BDC = x’dir.

Adım Adım Çözüm:

  1. Üçgen İç Açıları:
    Bir üçgendeki iç açıların toplamı her zaman 180°’dir. Öncelikle, bize verilen açıları kullanarak başlangıç yapalım.

  2. ABC Üçgeni:
    ∠BAC = 60°
    ∠BEC = 100°

    İç açıların toplamı her zaman 180° olduğu için, ∠ABC ve ∠ACB açıları toplamda 180° - 60° = 120° yapar.

  3. İç Açı Dağılımı:
    Şimdi, verilen ∠BEC açısı 100° olduğuna göre, B ve C noktalarının diğer açılarını bulmamız gerekiyor.

  4. D ve E Noktalarını İçeren Küçük Üçgenin Açıları:
    ∠BED + ∠EDC + ∠BDC = 180° olmalıdır.

    E noktası, açıortay olduğuna göre, ∠BDE = ∠EDC olacaktır.

  5. BDC Açıları Bulma:
    ∠BEC = ∠BDE + ∠EDC
    ∠BEC = 100° olduğundan;

    • ∠BDE = ∠EDC = 50° (çünkü 100° iki eşit parçaya bölünür: 50° + 50°)

  6. Üçgende İç Açıların Toplamı:

    ∠BDC = x açısını bulmamız gerekiyor. Bu açıyı hesaplarken:
    [
    ∠BDC = 180° - 50° - 50°
    ]
    [
    x = 180° - 100°
    ]
    [
    x = 80°
    ]

Sonuç:
m(∠BDC) = x açısı 80°’dir.

Bu şekilde, tüm adımları takip ederek ∠BDC açısının 80° olduğunu bulmuş olduk.