Soru sormak

YKS TYT YKS Geometri
1

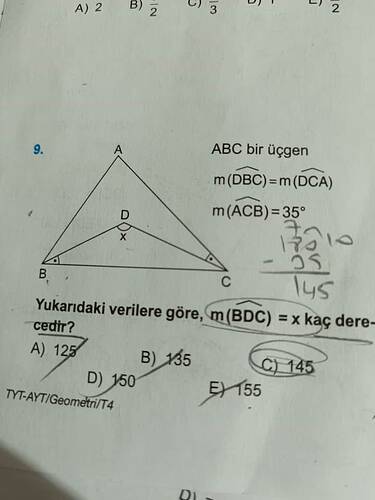
17268709199771909271986893036898
17268709199771909271986893036898720×960 27.9 KB

cevapla yollarmisiniz? cozerek

2

Yukarıdaki verilere göre, m(BDC) = x kaç derecedir?

Cevap:

ABC üçgeninde, verilere göre ( m(DBC) = m(DCA) ) ve ( m(ACB) = 35^\circ ).

Çözüm Adımları:

  1. Dış Açı Özelliği:

    • Üçgenin bir dış açısı, kendi iç açılarından birine eşit olan karşısındaki iki açının toplamına eşittir. Burada ( D ) noktasındaki dış açı olan ( x ) açısı, ( \angle BAC ) açısına eşit olur.

  2. Açılar Arasındaki İlişki:

    • Üçgende iç açıların toplamı ( 180^\circ ) olması gerektiğinden, ( \angle BAC + \angle ABC + \angle ACB = 180^\circ ) olur.
    • Verilenler: ( \angle ACB = 35^\circ )
    • Bu durumda, ( \angle BAC + \angle ABC + 35^\circ = 180^\circ )

  3. Dış Açıya Geçiş:

    • Bu durumda ( \angle BAC = 180^\circ - (\angle ABC + 35^\circ) )
    • Eğer ( x ) açısı, ( \angle BAC )'nin dış açısı ise, o zaman ( x = 180^\circ - 35^\circ ).

  4. Açının Hesaplanması:

    • ( x = 180^\circ - 35^\circ = 145^\circ ).

Sonuç olarak, ( x = 145 ) derecedir. Doğru cevap C) 145.