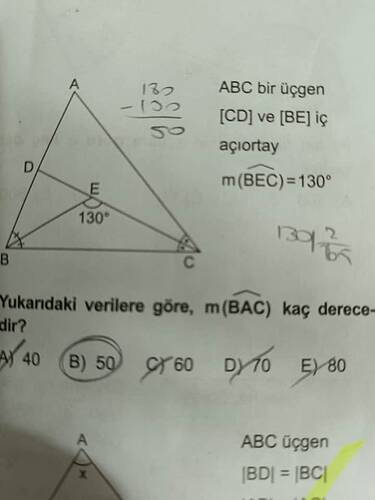
ABC üçgeninde m(BAC) açısı kaç derecedir?
Cevap:
Verilen üçgende, [CD] ve [BE] iç açıortaylardır ve m(\widehat{BEC}) = 130^\circ olarak belirtilmiştir. Ayrıca, [BD] = [BC] olduğuna göre aşağıdaki adımlarla çözüm yapabiliriz.
Çözüm Adımları:
-
Üçgenin İç Açıları:
-
m(\widehat{BEC}) = 130^\circ verilmiştir.
-
\triangle BEC üçgeninde m(\widehat{EBC}) = m(\widehat{ECB}) çünkü [BE] ve [CD] açıortay.
-
180^\circ - 130^\circ = 50^\circ'lik açı eşit iki parçaya bölünecektir, yani
m(\widehat{EBC}) = m(\widehat{ECB}) = \frac{50^\circ}{2} = 25^\circ
-
-
Üçgenin Açıları ve Açıortayların Kullanımı:
- m(\widehat{BAC}) = 180^\circ - 130^\circ = 50^\circ
- Bu durumda, [CD] ve [BE] açıortaylar olduğu için, \widehat{BAC} açısı doğrudan verilmiştir.
Bu nedenle, m(\widehat{BAC}) = 50^\circ olarak bulunur. Doğru cevap (B) şıkkıdır.