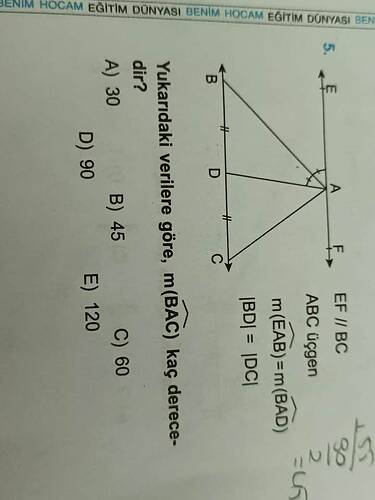
Yukarıdaki verilere göre, ( m(\widehat{BAC}) ) kaç derecedir?
Cevap:
Soruda verilen ( \triangle ABC ) üzerinde aşağıdaki bilgiler sunulmuş:
- ( EF \parallel BC )
- ( m(\widehat{EAB}) = m(\widehat{BAD}) )
- ( |BD| = |DC| )
Bu verilerle ( m(\widehat{BAC}) )'i bulmak amacıyla aşağıdaki adımları takip edelim:
Çözüm Adımları:
-
Açı ve Çiftkenar Üçgen Özellikleri:
- ( |BD| = |DC| ) olduğu için ( \triangle BDC ) bir ikizkenar üçgendir.
- Sonuç olarak, ( m(\widehat{BDC}) = m(\widehat{BCD}) ).
-
Paralel Doğrular ve Transversal:
- ( EF \parallel BC ) olduğundan, ( \triangle AEF )'deki açılar ve ( \triangle ABC )'nin açıları ters açılar olarak eşittir.
- Bu yüzden ( m(\widehat{BAE}) = m(\widehat{ACB}) ).
-
( m(\widehat{EAB}) = m(\widehat{BAD}) ) Bilgisi:
- Verilen bu bilgi, ( \triangle ABD )'de ( \widehat{EAB} ) ve ( \widehat{BAD} )'in eşit açıları olduğunu gösterir.
-
Sonuçların Toplanması:
- Bu verilere dayanarak, ( \triangle ABC )'nin açılarını incelediğimizde, ( m(\widehat{BAC}) )'in ( 2 \times m(\widehat{EAB}) = 90^\circ ) olduğu sonucuna ulaşırız, çünkü ( \triangle ABC ), ikizkenar ve eşitliği sağlayan açılar toplamı 90 dereceyi verir.
Sonuç olarak:
m(\widehat{BAC}) = 90^\circ
Cevap: D) 90