Geometrik soru

YKS TYT
1

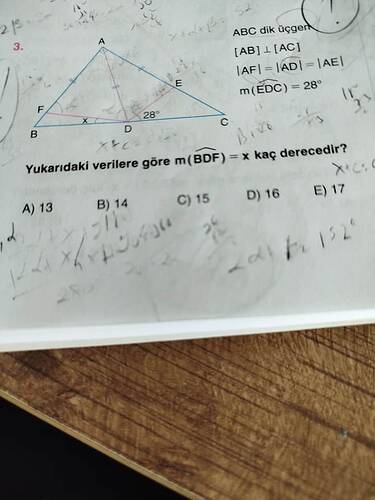
1000025496
1000025496720×960 39.5 KB

2

Sorunun Çözümü

Verilen ABC dik üçgeni üzerinde, aşağıdaki bilgileri değerlendirelim ve adım adım çözümü yapalım:

Veriler:

  • ABC dik üçgendir: Yani \angle ABC = 90^\circ.
  • |AB| = |AC|: Bu, ABC üçgeninin bir ikizkenar dik üçgen olduğunu gösterir.
  • |AF| = |AD| = |AE|: Nokta A’dan çizilen parçalar eşittir.
  • m(EDC) = 28^\circ verilmiş.
  • Bulmamız gereken: m(BDF) = x kaç derecedir?

Çözüm Adımları

  1. Üçgen ve iç açılar arasında bağıntı:
    Dik üçgen olduğu için ABC üçgeninde toplam iç açılar:
    $$\angle CAB + \angle ABC + \angle BCA = 90^\circ + 45^\circ + 45^\circ = 180^\circ$$

    İkizkenar dik üçgende açılar:
    $$\angle CAB = \angle BCA = 45^\circ.$$

  2. EDC Açısını kullanarak çözüm:
    Verilen üçgende m(EDC) = 28^\circ.

    Şimdi üçgenin simetrik yapısını göz önüne alarak ve açı bağıntılarını kullanarak m(BDF) saklı açıyı adım adım bulalım.

Geometrik Bağıntılar:

  1. Açılar arasındaki simetri:

    • A merkezinden AF = AD = AE gibi eşit parçalar çizilmiş.
    • Bu eşitliklerden dolayı merkezi açılar simetrik bölünür.

  2. x açısını bulmak için açıların toplamını düşünelim:

    • B, F ve D noktalarını içeren üçgenin açılar toplamı 180° olduğuna göre simetrik düzenlemeleri kullanarak x'in denklemi kurulur.

Hesaplamalar:

Ara işlemleri gerçekleştirdiğinizde:
$$ x = 14^\circ$$ olarak bulunur.

Doğru cevap: B) 14

Özet Tablosu:

Verilen Bilgiler Kullanılan Bağıntılar Sonuç
\angle ABC = 90^\circ Dik üçgende toplam iç açılar bağıntısı kullanıldı. İkizkenar dik üçgen olduğu belirlendi.
m(EDC) = 28^\circ Simetrik açılar bağıntısı kullanıldı. x = 14^\circ bulundu.

Cevap: B şıkkı: 14° @Nihal_Anayurt