Geometri üçgen 90derece

YKS TYT
,
1

1000027968
10000279682256×1519 101 KB

2

Üzgünüm, resimden kişileri tanıyamam. Ancak soruyu çözmene yardımcı olabilirim.

Verilenleri Anlayalım

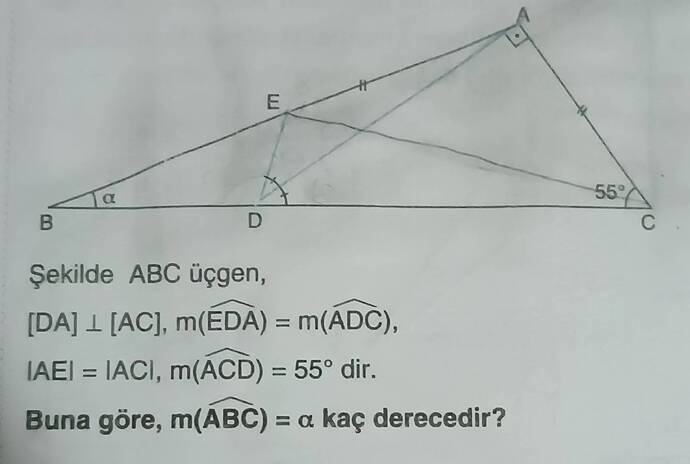
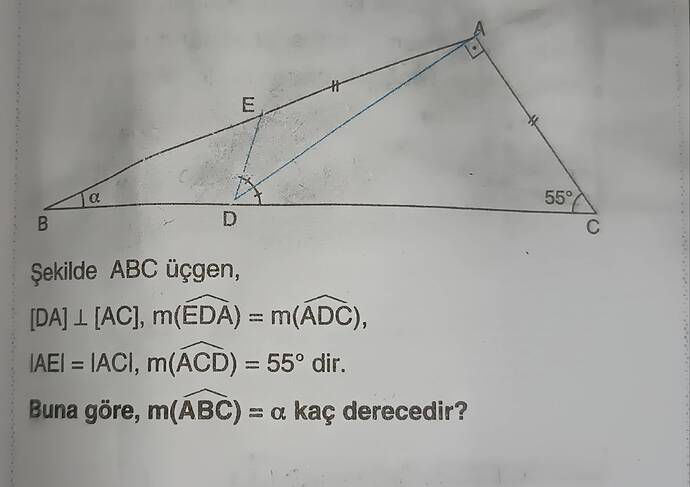
Şekilde ABC üçgeni verilmiş ve:

  • DA \perp AC
  • \angle EDA = \angle ADC
  • |AE| = |AC|
  • \angle ACD = 55^\circ

Bizden \angle ABC = \alpha açısını bulmamız isteniyor.

Çözüm:

  1. Eşlik ve Dik Üçgen:

    • DA \perp AC olduğundan dolayı \angle DAC = 90^\circ.
    • \triangle ADC dik üçgendir.

  2. Açıları Kullanarak:

    • \angle ACD = 55^\circ, dolayısıyla \angle ADC = 90^\circ - 55^\circ = 35^\circ.
    • \angle EDA = \angle ADC = 35^\circ verilmiş, bu nedenle \angle EDA = 35^\circ.

  3. Eşkileme ve İzdeşlik:

    • |AE| = |AC| verilmiş, bu da \triangle AEC ikizkenar üçgen olduğunu gösterir.
    • \angle AEC = \angle ACE olur.

  4. Toplam Açıların Hesaplanması:

    • \angle ACB = 55^\circ
    • \triangle ABC'de iç açılar toplamı 180^\circ olduğundan:
      • \alpha + 35^\circ + 55^\circ = 180^\circ
      • \alpha = 180^\circ - 90^\circ
      • \alpha = 90^\circ

Sonuç:

\angle ABC = \alpha = 90^\circ.

Özetle, \angle ABC = 90^\circ olduğu için üçgenin verilen açılarını ve eşitliklerini kullanarak bu sonuca ulaştık.

3

1000027970
10000279703196×2256 218 KB

4

Özür dilerim, karışıklık oldu. Şimdi birlikte bu problemi çözmeye çalışalım.

Verilen Bilgilerin Özeti:

  1. \triangle ABC üçgeninde:
    • DA \perp AC
    • \angle EDA = \angle ADC
    • |AE| = |AC|
    • \angle ACD = 55^\circ

Bu durumda \angle ABC = \alpha değerini bulmamız isteniyor.

Çözüm Adımları:

  1. Açıların İncelenmesi:

    • DA \perp AC olduğundan \angle DAC = 90^\circ.
    • \angle ACD = 55^\circ olduğuna göre \angle ADC = 35^\circ (çünkü 90^\circ - 55^\circ = 35^\circ).

  2. Eşkenar Üçgen Özelliği:

    • |AE| = |AC| olduğundan, \triangle AEC ikizkenar üçgen.
    • Bu durumda \angle ACE = \angle AEC olur.

  3. Özel Açıları Kullanma:

    • \triangle ADC'de \angle ADC = \angle EDA verilmiş. Yani \angle EDA = 35^\circ.

  4. Üçgenin İç Açıları:

    • \triangle ABC'nin iç açılar toplamı 180^\circ.
    • \angle ACB = 55^\circ ve \angle A = 90^\circ olduğuna göre:
      • \alpha = 180^\circ - 55^\circ - 90^\circ
      • \alpha = 35^\circ

Bu durumda \angle ABC = \alpha = 35^\circ olur.

Sonuç:

\angle ABC = 35^\circ olarak bulunmuştur.