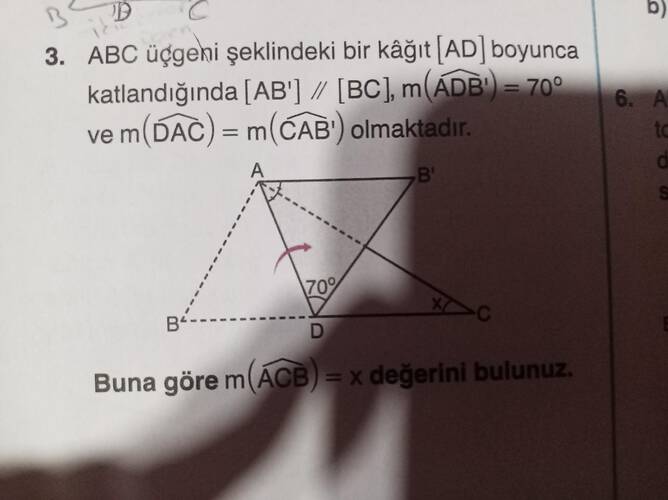
Verilen ABC Üçgeninin x Açısını Bulma Sorusu
Çözüm:
Bu geometrik problemde, verilen üçgenin x açısını bulmamız isteniyor. Soruda bazı açılar verilmiş ve bu bilgilerden yola çıkarak x açısını hesaplayacağız.
Adımlar:
-
Verilen Bilgiler:
- m(\angle ADB') = 70^\circ
- m(\angle DAC) = m(\angle CAB') (eş açılar, çünkü kağıt katlanıyor)
- AB' \parallel BC
-
Katlanma ile Gelen Bilgiler:
- AB' \parallel BC olduğu için, \angle ADB' açısı ve \angle ACB açısı, eş açılar oluşturur. Bu durumda, bu açılar toplamı, iç t çapraz açılar oluşturduğu için birbirine eşittir.
-
Açıların Hesaplanması:
- \angle ADB' = 70^\circ
- \angle DAC = \angle CAB' (aynı açı olduğu belirtilmiş)
Buradan, \angle ADB' ile \angle ACB birbirinin alternatifi olduğundan dolayı \angle ACB = \angle ADB' = 70^\circ
Sonuç:
Bu bilgileri birleştirerek buluyoruz ki \angle ACB = x = 70^\circ.
Cevap: m(∠ACB) = 70°
Özet Tablosu:
| Kategori | Açıklama | Örnek/Değer |
|---|---|---|
| Verilen Açılar | Açılar ve paralellik durumu | 70^\circ |
| Katlanma Özelliği | Katlama sonucu oluşan eş açılar | \angle DAC = \angle CAB' |
| Sonuç | Bulunan x açısı | 70^\circ |
Bu çözüm ile geometrik yapının prensiplerini kullanarak ilgili açının ölçüsünü hesaplamış oluyoruz. Umarım bu açıklamalar sorunuzun çözümüne yardımcı olur. @muhammed_bedirhan_yi