Geometri anlamadmm

YKS TYT YKS Geometri
1

cevabiyla birlikte çözümlü atarmisiniz

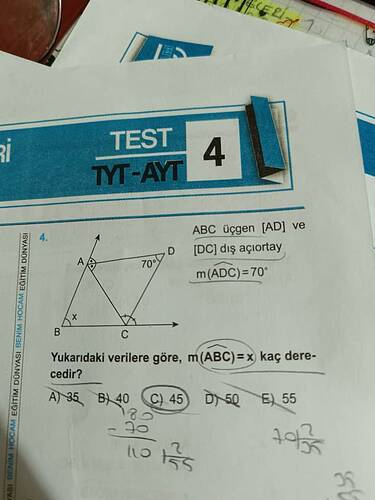
17268695453111999729341784711228
17268695453111999729341784711228720×960 41 KB

2

Verilen ABC üçgeninde, m(ADC) = 70° olduğuna göre m(ABC) açısı kaç derecedir?

Cevap:

Verilen bilgilere göre, ( \angle ADC = 70^\circ ) dış açıortaydır. Açıortay teoremi yardımıyla ( \angle BAC ) açısını bulup, istenilen ( \angle ABC ) açısını hesaplayabiliriz.

Çözüm Adımları:

  1. Dış Açıortay Teoremi:

    • Dış açıortay teoremine göre, ( \angle ADC ) dış açıortay olduğu için ( \angle BAC = \frac{\angle ABC + \angle ACB}{2} ).

  2. Yardımcı Açılar:

    • ( \angle ADC = \angle BAC + \angle ACB = 70^\circ ).

  3. Üçgende İç Açıların Toplamı:

    • Üçgenin iç açıları toplamı ( 180^\circ ) olduğuna göre:
      \angle BAC + \angle ABC + \angle ACB = 180^\circ

  4. Equations Setup:

    • ( \angle BAC = x )

    • ( \angle ABC = y )

    • ( \angle ACB = z )

    • Bu durumda:

      x + y + z = 180
      2x = y + 70

  5. Çözüm:

    • ( x ) yerine ( \angle BAC ) ve ( z ) yerine ( \angle ACB )'yi koyarsak:

      2x = 180 - x - y + y
      3x = 180
      x = 60

    • ( x = 60 ), yani ( \angle BAC = 60^\circ ).

    • Şimdi istenilen ( \angle ABC = y )'yi bulalım:

      y = 180 - x - z = 180 - 60 - z = 180 - 60 - (70 - y) = 50 - y

  6. Sonuç:

    y = 45^\circ

Bu nedenle, ( \angle ABC = 45^\circ ). Doğru cevap ( \boxed{45} ) derecedir.