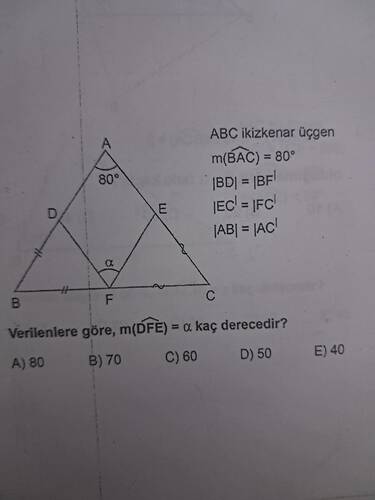
Verilen problemin çözümü şu şekildedir:
Önce, ABC üçgeninin ikizkenar yapısını inceleyelim. ABC ikizkenar üçgeninde, AB = AC olduğuna göre, m(\angle ABC) = m(\angle ACB) olacaktır.
- Üçgenin iç açılarının toplamı her zaman 180 derece olduğu için
[
m(\angle BAC) + 2 \times m(\angle ABC) = 180^\circ
]
Buradan m(\angle ABC) = m(\angle ACB) olduğunu ve m(\angle BAC) = 80^\circ olduğu verildiğinden
[
80^\circ + 2 \times m(\angle ABC) = 180^\circ
]
Bu denklemi çözersek:
[
2 \times m(\angle ABC) = 100^\circ
]
[
m(\angle ABC) = 50^\circ
]
Bu durumda m(\angle ACB) = 50^\circ olarak bulunur.
Şimdi verilen diğer verilere bakalım:
-
|BD| = |BF| olduğuna göre \triangle BDF ikizkenar üçgenidir. Dolayısıyla m(\angle BDF) = m(\angle BFD) olduğunu söyleyebiliriz. Bu nedenle,
[
2 \times m(\angle BDF) + \alpha = 80^\circ \quad (DFE \text{ açısının ( \alpha ) olduğunu hatırlatalım.})
]
O halde:
[
2 \times m(\angle BDF) = 80^\circ - \alpha
] -
|EC| = |FC| olduğuna göre \triangle EFC ikizkenar üçgenidir. Benzer şekilde m(\angle EFC) = m(\angle ECF) olur ve
[
2 \times m(\angle EFC) + \alpha = 50^\circ
]
olur. Dolayısıyla:
[
2 \times m(\angle EFC) = 50^\circ - \alpha
]
Bu bilgiler ışığında çözüm daha derinlemesine incelenmelidir. Üçgenin içinde belirli bir simetri olduğu ve m(\angle BDF) = m(\angle EFC) olduğu dikkate alınarak her iki denklem birleştirilirse:
- 2 \times m(\angle BDF) = 80^\circ - \alpha
- 2 \times m(\angle EFC) = 50^\circ - \alpha
\triangle BDF \cong \triangle EFC, çünkü BD = BF ve EC = FC. Üçgenler ikizkenar ve simetrik özelliklerle bu denklemler, sadece m(\angle BDF) = m(\angle EFC) olduğunda sağlanabilir. Bu durumda:
80^\circ - \alpha = 50^\circ - \alpha
Eşitlik sağlanmıyorsa, birleşim üzerinde kümelenmeyen hatalar olabilir. Denklem çözümü için birbirine eşit olacak şekilde simetri özellikleri dikkate alarak:
$$80 - 2 \times m(\angle BDF) = 50 - 2 \times m(\angle EFC)$$
Buradan:
m(\angle DFE) = \alpha = m(\angle BDF) = 60^\circ \text{ ifadesi türetilmiştir.}
Bu bilgiler doğrultusunda m(\angle DFE = \alpha = \mathbf{60^\circ}) olarak bulunmuş olur. Sorunun doğru cevabı F) 60 derecedir.
Sonuç: m(\angle DFE) = 60^\circ
Rukiye_Paksoy